Алгоритм полного решения транспортной задачи.
Таблица 30.
Таблица 29.
Таблица 28.
Проверим оптимальность этого плана. По занятым клеткам составим систему уравнений для определения потенциалов и решим ее, полагая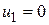 
. Затем запишем потенциалы (см. таблицу 29) и в этой же таблице высчитаем оценки свободных клеток.
| В А | ui | |||
| 0+(-1)-0<0 - | ||||
| 1+3-5<0 - | ||||
| -1+1-4<0 - | -1+(-1)-0<0 - | -1 | ||
| vj | -1 |
Все оценки отрицательны, значит, найденное опорное решение является оптимальным. Для завершения решения отбрасываем столбец с фиктивным
| потребителем, записываем итоговую таблицу 30, соответствующую исходному условию, и находим для построенного оптимального плана значение целевой функции:
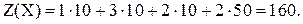Заметим, что на втором складе осталось 10 единиц продукции, но это связано с тем, что задача была открытой.
|
Подводя итог сказанному выше, определим порядок действий при решении транспортной задачи с M поставщиками и N потребителями.
1) Определить, является ли задача закрытой или открытой; в последнем случае ввести фиктивного потребителя или поставщика и построить новую таблицу.
2) Построить начальное опорное решение X1 (рекомендуется метод минимальной стоимости) и убедиться, что занято необходимое число клеток (M+N-1).
3) Найти потенциалы с помощью занятых клеток из неопределенной системы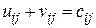 
((i;j) – адреса занятых клеток), а затем – оценки для свободных клеток 
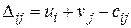(здесь (i;j) – адреса свободных клеток).
4) В случае, когда все оценки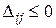 
, опорный план является оптимальным, и остается найти значение целевой функции f(X1). Если же среди оценок 
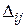оказались положительные, то выбираем ячейку с наибольшей положительной оценкой, строим для нее цикл и переходим к новому опорному решению X2. При этом должно выполняться неравенство f(X2)£ f(X1). Затем возвращаемся к п. 3) алгоритма.
5.6. Транспортная задача с ограничениями.Значительное количество экономических задач (порой не имеющих ничего общего с транспортировкой грузов) могут быть сведены к модели транспортной задачи. При этом величины cij могут означать стоимость, расстояние, время, производительность (см., например, [4, раздел D, п.6.14]). В то же время в самой транспортной задаче возникают различные ограничения (например, по критерию времени, при наличии особо важного потребителя – в открытой задаче это означает, что его запросы должны быть удовлетворены полностью). Ниже для примера рассматривается ситуация, когда вводятся ограничения на пропускную способность. При этом необходимо учитывать следующие правила.
Правило 1 (для ограничения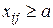 
). Перед решением задачи необходимо уменьшить запасы i-го поставщика и запросы j-го потребителя на величину a (резервируется перевозка 
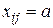). После решения задачи в оптимальном плане найденный объем перевозок 
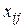увеличивается на величину a.
Правило 2 (для ограничения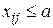 
). Перед решением задачи необходимо вместо j-го потребителя ввести двух потребителей. Первый, с номером j, будет иметь запрос a, второй, с номером N+1 (в таблицу добавляем новый, последний столбец) будет иметь запрос Bj-a. Стоимости в новом столбце совпадут с исходными за исключением i-й строки (в ней стоимость принимается равной сколь угодно большому положительному числу – это обеспечивает «не появление в ней перевозок»). После решения задачи в оптимальном плане объемы перевозок j-го и N+1-го потребителей суммируются.
Пример 5.7. Решить транспортную задачу с таблицей 5.31 и ограничениями:  ,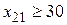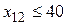 
|
|
Решение.Задача изначально является закрытой (и запасы, и запросы равны 200). В соответствии со сказанным выше запасы во второй строке и запросы в первом столбце уменьшаются на 30 (учтено условие 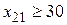). Далее во втором столбце запросы остаются равными 40, а мы достраиваем новый столбец с запросами 50-40=10. Стоимости в этом столбце совпадут с исходными, кроме ячейки в первой строке, куда запишем сколь угодно большое положительное число M. В результате нам нужно будет решать обычным способом (см. п. 5.5) транспортную задачу с таблицей 5.32. В таблице 5.33 приводится ее начальное опорное решение, найденное методом минимальной стоимости (читатель может провести построение сам).