Дисперсия случайной величины

Определение. Дисперсией случайной величины x называется число

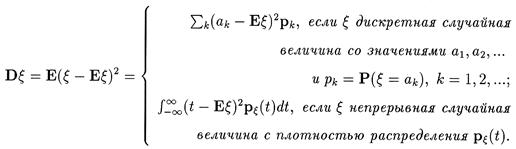Заметим, что величину m_k = E(x—Ex)^k, k ³ 2 называют центральным моментом порядка k случайной величины x.

 

Рассмотримсвойства дисперсии.

 

1). Dx= Ex² - (Ex)²

Действительно, из определения дисперсии получаем

 

2). Dx ³ 0, причем

Dx = 0 Û P(x = Ex) = 1,

т.е. x — постоянная (здесь Û - знак эквивалентности утверждений).

Так как Dx= E(x - Ex)², то Dx> 0. Пусть Р(x = Еx) = 1, тогда Ex² = (Ex)², и, следовательно, по свойству 1

Dx= Ex² - (Ex)² = 0

Если Dx= E(x - Ex)² = 0, то Р(x- Ex = 0) = 1 или Р(x= Ex) = 1, поскольку (x - Ex)² ³ 0.

Следствие. Если С—постоянная, то DC = 0.

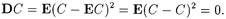Непосредственно из определения дисперсии получаем

3)

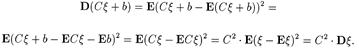D(Cx + b) = С² × Dx, где C u b постоянные. Доказывается следующим образом:

Следствие: D(Cx) = С² × Dx , D(x + b) = Dx.

4. Если x и h независимые случайные величины, тогда

Это свойство получается из определения дисперсии с учетом независимости случайных величин x и h. На самом деле,

поскольку если случайные величины x и h независимы, то случайные величины x — Еx и h — Еh также независимы (проверьте самостоятельно), поэтому по свойству 5 математического ожидания Е(x — Еx)(h — Еh) = 0.

Как следствие получаем: Если x₁, x₂, …, x_n независимые случайные величины, то