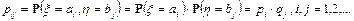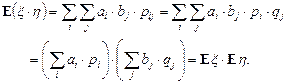Математическое ожидание случайной величины

Числовые характеристики случайных величин

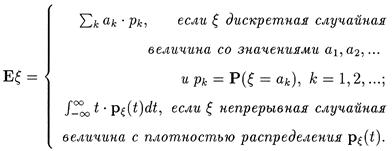Определение 1. Математическим ожиданием случайной величины x называется следующее число

 

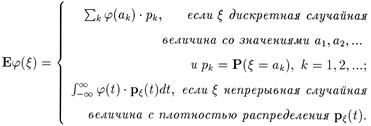Математическое ожидание называют еще средним значением величины и обозначают также через Мx. Заметим, что величину a_k = Еx^k, k > 0 называют начальным моментом (или просто моментом) порядка k случайной величины x. Для функции j(x) от случайной величины x (см. 2.3) математическое ожидание определяется так:

 

Для случайных величин, являющихся функциями f(x₁, x₂, …, x_n) от случайных величин x₁, x₂, ..., x_n математическое ожидание определяется так:

Рассмотримсвойства математического ожидания.

1. Если x постоянная величина, т.е. x = С с вероятностью 1, то Еx = С. Действительно, если x = С вероятностью 1, то по определению математического ожидания получаем Еx = С × 1 = С.

2. E(Cx)= С × Еx.

Это и последующие свойства докажем для дискретного случая.

Если x дискретная случайная величина со значениями а_k и вероятностями p _k = Р(x = а_k), k = 1,2,..., то согласно пункту 2.3 Сx является дискретной случайной величиной со значениями Са_k и теми же вероятностями p_k, k = 1,2,... Тогда по определению математического ожидания получаем

 

 

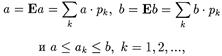и получаем требуемое.

4. Е(x + h) = Ex + Еh.

Пусть случайные величины x и h имеют следующие таблицы распределения:

и

Тогда

 

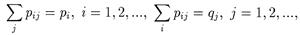поскольку (см. 2.4.2)

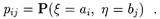где

 

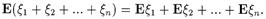Как следствие получаем

 

5. Если x и h независимые случайные величины, тогда

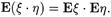Пусть x и h случайные величины, введенные в свойстве 4. Как показано в 2.4.3 для независимых случайных величин x и h выполняются равенства