Вероятности
Пусть некоторый эксперимент повторяется п раз (т.е. проводится серия из п одинаковых и независимых друг от друга экспериментов). Фиксируем случайное событие А и предполагаем, что это событие появлялось nn(A) раз. Рассмотрим отношение nn(A)/n, которое называется частотой события А в данной серии. С ростом п колебания этого отношения вокруг некоторого постоянного числа Р(А) все меньше и в различных сериях практически совпадают при больших n, т.е. nn(A)/n » Р(А). Итак, событию А сопоставляется численная характеристика Р(A), которая и называется вероятностью события А. Такую трактовку понятия вероятности называют частотным или статистическим определением вероятности.
Теперь приведем аксиомы теории вероятностей.
Пусть W — пространство элементарных событий, F — s-алгебра событий, Â1 – пространство действительных чисел.
Определение 1. Вероятностью называют числовую функцию Р(А), определенную на s-алгебре событий F, т.е. Р : F ® Â1, которая удовлетворяет следующим аксиомам.
Аксиома 1. Для любого события А из F число Р(А) ³ 0.
Аксиома 2. Вероятность достоверного события W равна 1, т.е. P(W) = 1.
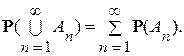 |
Аксиома 3. Пусть A1, А2,..., An,... — счетная последовательность попарно несовместных событий, т.е. Аi Ç Аj = Æ для i ¹ j, тогда
Определение 2. Вероятностным пространством называется тройка объектов (W,F,Р), где W — непустое пространство элементарных событий, F— s-алгебра событий из W, Р— вероятность, определенная на F.
В дальнейшем, для удобства записи, знак суммы 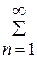 будем записывать как
будем записывать как  или Sn , а знаки
или Sn , а знаки 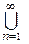 - как
- как 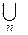 или
или 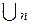 ;
;  - как
- как 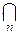 или
или 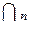 .
.