Решение задачи вычисления длины наибольшей общей подпоследовательности

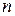Пусть – последовательность символов . Последовательность называется подпоследовательностью последовательности если она может быть получена из последовательности удалением ее некоторых элементов. Например, если – последовательность символов то последовательность состоящая из символов является подпоследовательностью так как она может быть получена с помощью удаления элементов

Подпоследовательность называется общей подпоследовательностью последовательностей и если она является подпоследовательностью обеих последовательностей. Например, подпоследовательность является общей подпоследовательностью последовательностей и

Длиной последовательности (подпоследовательности) будем называть количество ее элементов. Например, длина последовательности равна 6.

Подпоследовательность называется наибольшейобщей подпоследовательностью последовательностей и если имеет наибольшую длину среди всех общих подпоследовательностей. Например, общая подпоследовательность является наибольшей для последовательностей и В общем случае может быть несколько наибольших подпоследовательностей. Например, тоже является наибольшей общей подпоследовательностью для последовательностей из последнего примера. Часто для обозначения наибольшей общей подпоследовательности используется сокращение LCS (longest common subsequence).

Рекурсивный алгоритм вычисления длины LCS для двух последовательностей и основывается на трех следующих очевидных утверждениях, которые приводятся без доказательства:

1. Если то и является LCS для и

2. Если и то является LCS для и

3. Если и то является LCS для и

Обозначив через длину LCS для последовательностей и можем записать следующее рекуррентное соотношение:

Рассмотрим пример вычисления длины LCS для последовательностей и Вычисление осуществляется по шагам:

1) .

4) .

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

21)

22)

23)

24)

25)

26)

Все шаги вычисления можно разбить на две группы: с 1 по 17 и с 18 по 26. Первая группа соответствует рекурсивному погружению, вторая – восходящему вычислению. Результатом вычисления является значение равное длине LCS. Нетрудно убедиться, что для последовательностей и существуют две LCS: и имеющих длину 3.

На рис.13 и 14 представлена рекурсивная функция lcs, вычисляющая длину LCS для двух заданных последовательностей, а на рис. 15 – пример программы, вызывающей эту функцию, и результат ее выполнения (рис. 16) соответственно.

Рис. 13. Прототип функции lcs, вычисляющей длину LCS для двух заданных последовательностей

Рис. 14. Реализация функции lcs

Рис. 15. Пример вызова функции lcs

Рис. 16. Результат выполнения программы, представленной на рис. 15

Функция lcsимеет четыре параметра: lenx (длина первой последовательности), x(массив, содержащий символы первой последовательности), leny (длина второй последовательности), x(массив, содержащий символы второй последовательности). Функция возвращает длину LCS заданных последовательностей.

Функция lcs фактически повторяет запись рекуррентного соотношения, записанного выше, и поэтому не требует дополнительного пояснения. Обратите внимание, что исходные последовательности и результат совпадают с последовательностями и результатом вычисления предыдущего примера.