Анализ последовательной цепи переменного тока

Емкостной элемент.

Индуктивный элемент.

UR(t)

Активное сопротивление.

 

u(t) = U_msinωt

iR(t)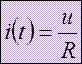

 

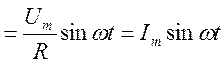
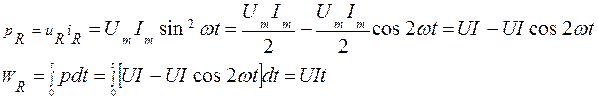
iL(t) i(t) = I_m sinωt

UL(t)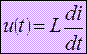

 

 

ic(t) u(t) = U_m sinωt

 

Uc(t)

 

 

 

Мы показали, что при заданном токе напряжения на пассивных элементах будут следующими:

 

 

 

 

 

 

Все рассмотренные элементы объединим в последовательную цепь (рис.4.1) ток в ней известен. Определим параметры мгновенного значения ЭДС.

 

Неизвестная ЭДС также будет иметь вид гармонической функции.

 

 

Рис.4.1.

-

Данное выражение представляет собой уравнение для электрической цепи, записанное по II закону Кирхгофа (для установившегося режима).

Полагая, в частности, ωt = π/2 и ωt = 0, получим RI_m = U_mcosφ; (ωL – 1/ωC)I_m = U_msinφ.

Возведя первое и второе равенства в квадрат и сложив, получим:

[R² + (ωL – 1/ωC)] I_m² = U_m²

Откуда находим связь между амплитудами тока и напряжения:

 

 

 

 

Если в той же последовательной цепи заданной будет ЭДС: e(t) = E_msinωt, то i(t) = I_msin(ωt ± φ).

 

 

Полученные соотношения можно использовать для расчёта мгновенных значений напряжения и тока в последовательной цепи, питаемой от источника гармонической ЭДС.

 

Рассмотрим несколько примеров.