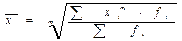Пример 1.

Имеются данные о размере прибыли на одну торговую точку предприятия за год (млн.руб).

8,0 8,2 8,5 8,5 8,7 8,8 8,8 8,9 10,1 10,5

10,5 10,7 11,0 11,0 11,6 11,6 11,8 11,8 12,1 12,1

12,3 12,4 12,4 12,5 12,5 12,7 12,8 12,8 12,8 12,8

13,1 13,1 13,5 13,5 13,7 14,1 14,2 14,2 14,5 14,5

14,6 14,6 15,2 15,2 15,4 15,7 15,9 16,2 16,2 16,2

16,9 16,9 17,5 17,5 18,5 19,0 19,5 19,5 20,1 22,0

Составим типологическую группировку (табл.3.) торговых точек предприятия по размеру получаемой прибыли.

R= (Xmax-Xmin) = 22-8 = 16

k= 1+3,32* lg N = 1 + 3,32* lg 60 = 7 ( количество групп)

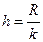,(величина интервала)

Таблица3.

Группировка торговых предприятий

 

Объем прибыли (млн.руб) хi	Количество торговых точек fi	Накопленные частоты S
8-10
10-12
12-14
14-16
16-18
18-20
20-22
Итого

 

При больших объемах единиц совокупности и неравномерности распределения признака как правило используют группировки с неравными интервалами, тогда размеры интервалов определяются аналитиками самостоятельно на основе имеющегося опыта.

Следует отметить, что в любом случае процесс группировки данных включает несколько этапов:

- выбор группировочного признака;

- упорядочивание совокупности по этому признаку;

- определение количества групп;

- определение границ интервалов.

Основное правило при проведении группировки состоит в следующем: не должно быть пустых и малозаполненных интервалов. Иными словами, формула Стерджесса дает лишь ориентировочные значения интервалов группировки; при принятии окончательного решения, как правило, значения округляются или незначительно меняются.

В экономическом анализе достаточно часто используются структурные и аналитические группировки. Структурные группировки предназначены для изучения структуры и состава изучаемого явления, происходящих в нем сдвигов относительно выбранного варьирующего показателя. Аналитические группировки предназначены для изучения взаимосвязей между двумя и более показателями, характеризующими данную совокупность. Один показатель при этом рассматривается как результат, а остальные как факторы. С помощью данного вида группировок можно рассчитать тесноту связи между результативным и факторными признаками. Однако процесс построения аналитических группировок достаточно трудоемок и не всегда приводит к желаемым результатам. В современных условиях данная проблема решается с применением вычислительной техники и использования методов построения многомерных группировок (подробнее методика многомерных группировок будет показана при рассмотрении метода кластерного анализа).

4.2. Метод средних величин

В любой совокупности экономических явлений или субъектов наблюдаются различия между отдельными единицами этой совокупностью. Одновременно с этими различиями существует и нечто общее, что объединяет совокупность и позволяет отнести все рассматриваемые субъекты и явления к одному классу. Роль средних величин заключается в обобщении, то есть замене множества индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений. Средняя величина обобщает качественно однородные значения признака и, следовательно, является типической характеристикой признака в данной совокупности. Средние величины делятся на степенные и структурные.

Степенная средняя, в зависимости от степени “m”, может представлять собой различные виды средних величин.

x_i – значение показателя

m – номер степени средней

n - число вариант

 

C помощью выше приведенной формулы могут быть рассчитаны показатели только при трех условиях, если: вариационный ряд короткий; значения признака не сгруппированы и варианты встречаются одинаковое число раз.

Если варианты встречаются неодинаковое число раз, то средние величины рассчитываются не как простые, а взвешенные по следующей формуле: