Тень внутри полой полусферы на фасаде
Тень внутри полой полусферы на фасадепоказана на рис. 21. Тень эта, падающая от полукруглого ребра DAK,получается в форме полуэллипса k'b'd',так как она есть результат пересечения поверхности
сферы таким лучевым цилиндром, который входит в сферу по плоской кривой DAK (см. рис. 22). Линияd'k'есть большая ось эллипса; размер же малой полуоси о'b'получается примерно в ⅓ R.Это можно доказать следующим образом. Если полукруглое сечение полусферы плоскостью Р,включающей луч, проходящий через точку А,совместить с фронтальным сечением полусферы путем вращения вокруг диаметра АС,то это сечение займет положение a'k'c'(при вращении полукруга вверх), причем сам луч займет положение а' b'1 под углом 35° к диаметру а'с'.
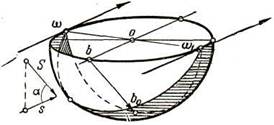 Рис. 22
Рис. 22
При обратном вращении полукруга точка b'1попадет в точку b', поскольку она будет в пространстве описывать дугу окружности, плоскость которой перпендикулярна к фронтальной оси вращения а'с'.
Если соединить точки о' и b1', то <b1'o'c' = 70°, так как он является внешним по отношению к ^a'o'b1',имеющему два угла по 35° (о'а' = о'b' = R).Следовательно, o'b' = R соs 70°≈ ⅓ R.