ТЕНИ ПОВЕРХНОСТЕЙ ВРАЩЕНИЯ С КРИВОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ

1.6.1.Тень шара

Тень шара,собственная и падающая, на Ни Vпоказана на рис. 20.

Рис. 19

Если обратиться сначала к пространственному изображению шара (рис. 3), то нетрудно представить, что цилиндр лучей обертывает шар по окружности большого круга. Эта окружность находится в наклонной (по отношению к Ни V) плоскости и будет проектироваться на Ни Vодинаковыми эллипсами (поскольку лучи света идут по диагонали куба, одинаково наклоненной к плоскостям Ни V). Тот же обертывающий цилиндр лучей будет пересекаться плоскостями Ни Vпо эллипсам одинакового размера.

Стало быть, построение собственной и падающих на Ни Vтеней шара сводится к построению двух одинаковых эллипсов на проекциях шара (собственная тень) и двух других одинаковых эллипсов на плоскостях Ни V(падающие тени шара). Рассмотрим в подробностях построения тени на Н.

Чтобы получить проекцию окружности касания лучевого цилиндра к поверхности. шара в виде одной прямой линии, заменим плоскость V вертикальной плоскостью V_1,поставленной параллельно лучам света. В таком случае плоскость окружности касания Рбудет перпендикулярна к лучу света и, следовательно, будет вертикально-проектирующей плоскостью; ее следы на эпюре: Рhи Pv1.

При таком положении плоскости V1 как видно, представляется возможным получить на плане малую ось эллипса 1—2 на проекции шара и большую ось 1₀2₀эллипса падающей тени. Вместе с тем, можно определить аналитически размеры этих осей в зависимости от радиуса шара R.Именно, малая полуось 1сэллипса на проекции шара, равная катету 1'1b прямоугольного треугольника 1'1bс'1, равна радиусу шара R,умноженному на sin 35° (1с = 1'1b= R sin 35°).

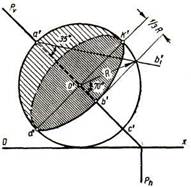Рис. 21

Это потому, что на плоскости V_lугол наклона луча света к плоскостям проекций, а именно— угол с₁'с₀' 1₀', виден в натуральную величину, а угол 1'1с'1b равен углу с₁' с₀' 1₁', как имеющий с ним взаимно перпендикулярные стороны. А так как известно, что sin 35°≈ tg 30°, то точки 1 и 2на плане шара, являющиеся концами малой оси эллипса, можно

найти, не пользуясь проекцией шара на плоскости V.Для этого надо вписать в окружность правильный треугольник 3—5—6,взяв за вершину 3конец большой оси этого эллипса. Тогда: lc=c3tg30°, потому что половина угла такого треугольника равна 30°.

Видно далее, что, не пользуясь проекцией шара на V1, можно построить и большую полуось М_с — 2o эллипса падающей тени, так как М_с2₀ = с_о'2o' =

А так как высота М_o2_oравностороннего Δ3₀2₀4₀при стороне 2R равняется также 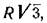то выходит, что для определения длины большой полуоси М_с2₀надо на линии 3₀4₀,как на стороне, построить правильный треугольник 3₀4₀2_o;тогда вершина его 2₀и будет представлять конец искомой полуоси. Вместе с тем, следует заметить, что и точку М_с— тень на Hот центра Сшара — можно построить на плане, не пользуясь фасадом шара на V,если известна отметка центра, т. е. апликата Z_c.Видно, что для этого надо отрезок Z_cотложить от точки ссперва по вертикали, а затем вправо по горизонтали.

Поскольку, как выше отмечалось, собственная и падающая тени шара на вертикальной и горизонтальной проекции тождественны, построение тени на Vсводится к повторению только что описанных операций для Н; при этом следует учесть, что можно точку N_c— тень на Vот центра шара—найти, не пользуясь планом, если известен вынос (координата Y_c) центра шара. Как видно, для этого надо от с'отложить Y_ссначала вправо по горизонтали, а затем вниз по вертикали. При правильном построении падающих теней эллипсы на Ни Vмогут пересекаться только в точках, лежащих на оси Ох.