Напряженность поля точечного заряда

Напряженность электрического поля (М. Фарадей 1850 г)

Согласно современным представлениям, электромагнитное взаимодействие между телами осуществляется посредством поля. (Это представление лежит в основе так называемой классической электродинамики, к изучению которой мы приступаем. В квантовой теории все силы природы возникают в результате обмена частицами-переносчиками между взаимодействующими частицами. В случае электромагнитного взаимодействия такими частицами-переносчиками являются фотоны - кванты электромагнитного поля).

Определение заряда и напряженности электрического поля, как и любых других физических величин, сводится к указанию принципиального способа их измерения. Так как электромагнитные явления связаны с действием сил на заряженные тела, то именно силы могут быть положены в основу этих определений.

Для изучения действия сил на заряженные тела будем использовать пробный заряд.

Пробным зарядом называется электрически заряженное тело, удовлетворяющее следующим требованиям:

1) величина заряда должна быть настолько мала, чтобы практически не приводить к перераспределению электрического заряда на телах, поле которых исследуется с помощью пробного заряда;

2) размеры пробного заряда должны быть настолько малы, чтобы все его части были погружены в точки, где исследуемое поле одинаково (т.е. в области, занимаемой телом пробного заряда, исследуемое поле однородно).

Заряды, удовлетворяющие второму условию, называются точечными.

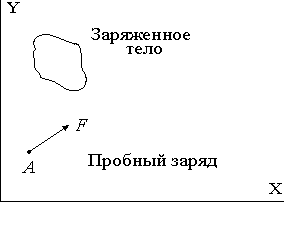
Рис.1.1. Действие заряженного тела на неподвижный в системе отсчета XY пробный заряд

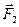Возьмем два таких пробных заряда и поместим их по очереди в одну и ту же точку пространства так, чтобы они покоились в соответствующей инерциальной системе отсчета (рис.1.1). Пусть и - силы, с которыми заряженные тела действуют на эти неподвижные пробные заряды. Обобщением опытных фактов является следующее утверждение: силы и 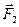имеют либо одинаковые, либо противоположные направления, а отношение их величин F₁/F₂ не зависит от выбора точки наблюдения (т.е. точки расположения пробного заряда). Поэтому ясно, что отношение F₁/F₂ служит мерой самих пробных зарядов, а не действия заряженных тел, и состояние электризации пробного заряда можно охарактеризовать скалярной величиной , определив его как

(1.1)

Из этого уравнения следуют два важных вывода:

1) приняв заряд какого-либо пробного тела за положительный единичный, из (1.1) можно найти величину второго заряда;

2) помещая данный пробный заряд q₁ (например, тот, который выбран за положительную единицу) в разные точки пространства А, В, С, ... и измеряя силы , действующие на него, когда он неподвижен, можно с помощью (1.1) определить силы 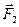, с которой будут действовать заряженные тела на любой другой неподвижный пробный заряд q₂, помещаемый в эти точки. В самом деле, .

Другими словами, множество сил, действующих на единичный неподвижный пробный заряд во всех точках пространства данной системы отсчета, является силовым полем, которое в то же время предопределяет силу, действующую на любой другой заряд, неподвижный в этой системе отсчета.

Для описания силовых свойств электрического поля вводится напряженность электрического поля .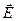

Векторная физическая величина, модуль которой численно равен силе, действующей на единичный положительный неподвижный пробный заряд, помещенный в некоторой точке наблюдения, а направление совпадает с направлением этой силы, называется напряженностью электрического поля в рассматриваемой точке наблюдения и обозначается вектором ,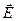

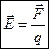(1.2)

Силу, действующую на любой другой заряд q, покоящийся в поле 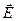, на основании (1.1) и (1.2), представим в следующем векторном виде:

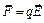
Неподвижность заряда q очень существенна, так как электромагнитное взаимодействие зависит не только от заряда тела, но и от скорости его движения. Электрическое же (а не электромагнитное) поле полностью описывает взаимодействие зарядов только по отношению к таким системам отсчета, где заряженные тела неподвижны.

Рис.1.2

Если вспомнить наш первый рис. (по выводу закону Кулона) и совместить начало вектора 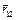с положением заряда q_1, который обозначим просто q, то на основании определения вектора и закона Кулона, запишем

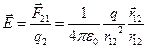(1.4)

Рис.1.3. Зависимость величины напряженности электрического поля точечного заряда от расстояния до точки наблюдения

На рис.1.3 приведена (в условных единицах) зависимость модуля напряженности электрического поля, созданного точечным зарядом, от расстояния между точечным зарядом и точкой наблюдения, фактически это график функции

,

которую легко получить из формулы (1.4), положив.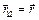

На рис.1.4 в некотором условном масштабе изображены поля векторов напряженности 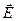, созданные положительным и отрицательным электрическими точечными зарядами. Существенным недостатком такого способа изображения силового векторного поля 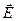является наложение векторов напряженности друг на друга, особенно вблизи источника. На рис.1.4 этого удалось избежать благодаря специальному выбору точек наблюдения, в которых изображены векторы поля.

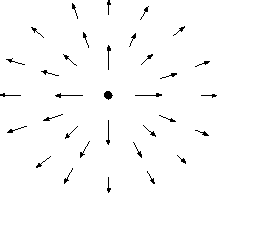
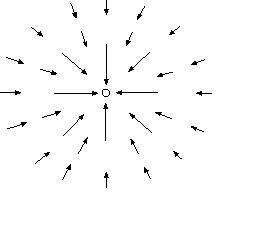
а) б)

Рис.1.4. Изображение векторного поля 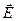: а - положительного точечного заряда; б - отрицательного точечного заряда

Иногда для изображения силового поля удобнее использовать не векторы 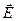, а линии поля (силовые линии).