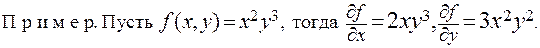ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Подведение итогов. Ответы на вопросы учащихся. Заполнение анкет.
Если систематически употребляя алкоголь с друзьями, вы не наносите вред никому кроме самого себя, то откуда же все эти данные. Кто ездит в нетрезвом виде, кто воспитывает пьющих детей, кто в состоянии алкогольной интоксикации совершает преступления, кто, в конце концов, забросал все парки и заповедники страны бутылками и окурками? Неужели ничтожный процент алкоголиков (приблизительно 2.1 %) натворили все это в нашей стране?
Помните, что каждым вашем поступком вы закладываете фундамент не только своей будущей жизни, но и жизни всего нашого народа. Живите трезво! Ради светлого будущего вас, ваших детей, внуков, вашей страны.
Мы знаем способ нахождения наибольшего или наименьшего значения функции одной переменной и способ иллюстрации функциональной зависимости с помощью графика. При решении технических задач часто приходится иметь дело с зависимостью исследуемой величины от многих переменных. Например,  – функция трех независимых переменных.
– функция трех независимых переменных.
Если график функции одной переменной представляет собой плоскую кривую, характеризующую зависимость функции от переменной, то в случае двух переменных такую характеристику зависимости функции ( ) от переменных (
) от переменных ( и
и 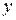 ) выражает поверхность.
) выражает поверхность.

Покажем, как изобразить такую поверхность графически, если областью определения функции двух переменных является прямоугольник. Например, построим с помощью пакета программ MAXIMA график функции  Для этого введем команду plot3d(x^3-2*y^2,[x,-2,2],[y,-1,1])инажмем клавиши Shift+Enter. Мы получим следующую картину.
Для этого введем команду plot3d(x^3-2*y^2,[x,-2,2],[y,-1,1])инажмем клавиши Shift+Enter. Мы получим следующую картину.
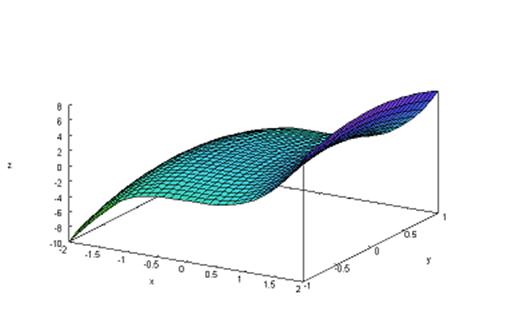
Для графического изображения зависимости функции трех и более переменных понадобилось бы пространство размерности, большей, чем 3. Поэтому такие графические изображения невозможны.
Следовательно, мы должны познакомиться со способом нахождения наибольшего или наименьшего значения функции нескольких переменных без использования визуальной иллюстрации. Большую роль в исследовании функции нескольких переменных играют частные производные.
Дифференцируемость функции двух переменных  в некоторой точке означает, что приращение функции в этой точке отличается от некоторой линейной комбинации приращений каждой из переменных на величину большего порядка малости, чем приращение каждой переменной:
в некоторой точке означает, что приращение функции в этой точке отличается от некоторой линейной комбинации приращений каждой из переменных на величину большего порядка малости, чем приращение каждой переменной: 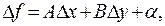 где
где 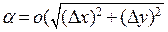 .
.
Числа Aи B, участвующие в условии дифференцируемости, называются частными производными первого порядка и обозначаются 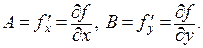
Взять частную производную, например, по переменной x– это значит, считая yпостоянной, рассматривать исходную функцию как функцию одной переменной xи взять производную от функции по этой переменной.