Двухмассовая модель механической части силового канала электропривода

Математические модели механической части силового канала электропривода

Лекция 5

Для того чтобы описать поведение электропривода в статических и динамических режимах необходимо представить удобную и точную математическую модель. Существует два вида представления математических моделей механической части силового канала электропривода:

1) Двухмассовая модель. Этот вид является наиболее универсальным и точным, однако при этом достаточно сложным.

2) Одномассовая модель.

 

Двухмассовая модель представлена на рисунке 1.14 в виде двух вращающихся масс, связанных между собой упругой механической связью.

Первая вращающаяся масса (электродвигатель) обладает моментом инерции J₁ и создает вращающий электромагнитный момент М. При этом вал электродвигателя вращается с угловой скоростью ω₁. Электродвигатель связан с помощью вала, обладающего жесткостью С, с производственным механизмом, имеющим момент инерции J₂ и вращающимся в направлении вала двигателя с угловой скоростью ω₂. При этом механизм создает статический момент сопротивления М_С2, направленный против вращения. Кроме того, сам двигатель создает статический момент сопротивления М_С1. Угол скручивания вала со стороны двигателя равен , а со стороны механизма – .

 

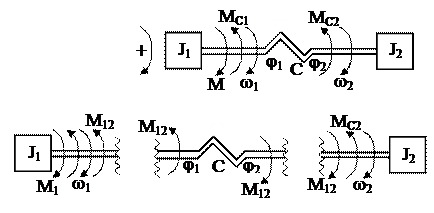Рисунок 1.14- Двухмассовая модель механической части силового канала электропривода

 

Запишем систему уравнений, которая будет являться математическим описанием представленной модели и будет описывать механические процессы, происходящие в ней. Для этого применим известный из механики метод, заключающийся в том, что вся система мысленно расчленяется на отдельные составляющие, а реальные связи между этими составляющими заменяются их воздействиями. Расчленим модель на три составляющие как показано на рисунке 1.14.

Первое уравнение для упругой связи запишем в соответствии с законом Гука

, (1.5)

где М₁₂ – момент упругости.

Уравнения для первой и второй вращающихся масс по второму закону Ньютона имеют вид

, (1.6)

. (1.7)

Уравнения (1.6) и (1.7) представляют из себя дифференциальные уравнения первого порядка. Поэтому для того чтобы привести все три уравнения к единому виду продифференцируем уравнение (1.5)

 

,

где ω₁₌, ω₂=

 

Тогда получим

.

Таким образом, получили систему трех дифференциальных уравнений первого порядка, которые описывают механические процессы, происходящие в силовом канале ЭП, и носят названиедвухмассовая модель механической части силового канала ЭП.