Тени геометрических тел
При построении теней геометрических тел сначала следует определить контур собственной тени, а затем приступить к построению падающей тени, которая является тенью контура собственной тени.
Тень призмы(рис. 7). Задняя и правая боковая грани призмы находятся в собственной тени. Ребра, разделяющие освещенные и затененные грани призмы, образуют контур собственной тени. Они представляют собой прямые частного положения, падающие тени от которых строятся просто (см. рис. 5). Ширина падающей тени на фасаде от столба прямоугольного поперечного сечения равна сумме сторон плана.
Тень цилиндра(рис. 8). Контур собственной тени определяется двумя образующими 1 и 5, по которым лучевые плоскости касаются его боковой поверхности. Фронтальная проекция контура собственной тени может быть определена без плана с помощью равнобедренного треугольника с засечкой на гипотенузе, построенного на половине фронтальной проекции основания. Это относится и к цилиндру, расположенному горизонтально (рис. 6,г). Построение падающей тени на плане и фасаде включает уже известные элементы - построение тени горизонтальной окружности и теней вертикальных прямых.
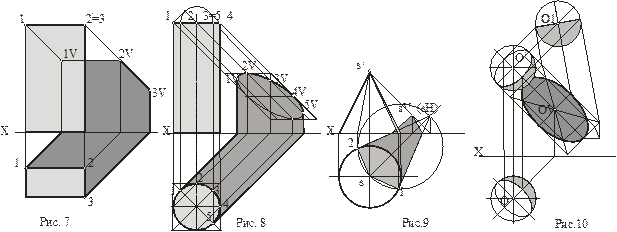
Тень конуса(рис. 9). При построении тени конуса сначала строят падающую тень, с помощью которой определяют затем контур собственной тени. Начинают с построения падающей тени вершины на плоскость основания конуса. Такой тенью является мнимая тень sH. Касательные, проведенные из этой точки к основанию конуса, определяют теневые образующие конуса, которые и являются контуром собственной тени. Точки касания графически точно определяются с помощью окружности, построенной на проекции падающей тени s-sH высоты конуса. Контур собственной тени конуса - линия касания боковой поверхности конуса лучевыми плоскостями, параллельными световым лучам, а контур падающей тени - горизонтальные следы лучевых плоскостей.
Тень сферы(рис. 10). Световые лучи, касающиеся поверхности сферы, образуют обертывающую цилиндрическую лучевую поверхность. Она касается сферы по большой окружности-контуру собственной тени сферы. Проекциями контура собственной тени являются эллипсы. Большая ось эллипса равна диаметру сферы, а малая ось 0,61D. Чтобы определить этот параметр, можно применить замену плоскости проекции H и построить новую проекцию сферы и ее собственную тень на плоскости проекций, параллельной лучам света. В этом случае при истинном наклоне луча (35°) новая проекция контура собственной тени будет перпендикулярна проекциям лучей (графическое построение угла в 35° показано на дополнительной проекции). Построение падающей тени сферы на фронтальную плоскость проекций понятно из чертежа.

На рисунке 11 показан пример построения собственных и подающих теней капители.
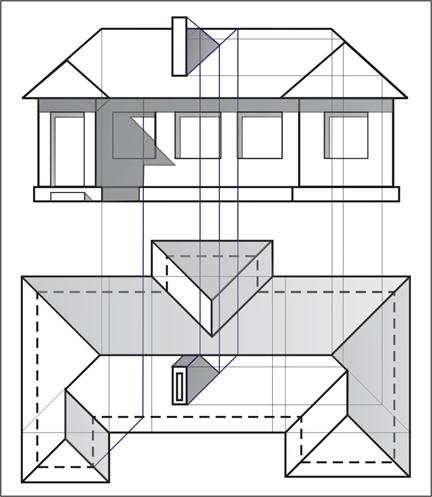
Рис. 12. Пример построения теней на фасадах и на плане крыши