Дроссели для импульсных источников питания на ферритовых кольцах

При повторении импульсных вторичных источников питания и стабилизаторов напряжения или самостоятельной их разработке радиолю-бители испытывают трудности при подборе магнитопроводов и расчете индуктивных элементов устройств. В [99] приведены рекомендации, кото-рые могут помочь в решении таких задач.

В однотактных импульсных источниках питания и стабилизаторах напряжения важнейшим элементом является дроссель или импульсный трансформатор, в котором происходит накопление энергии. Обычно их наматывают на броневых или Ш-образных ферритовых магнитопроводах с зазором или кольцах из магнитодиэлектрика П140 или П160 [85-99]. И те и другие магнитопроводы достаточно дороги и дефицитны. В то же время в большинстве случаев индуктивные элементы таких устройств можно выполнить на широко распространенных кольцах из феррита с проницаемостью 600…4000, если в них ввести зазор.

Индуктивность L катушки, намотанной на кольцевом магнитопроводе, как известно, можно найти по формуле [] L = ALN2, где AL – так называемый коэффициент индуктивности, N – число витков катушки. Коэффициент AL соответствует индуктивности катушки в один виток и обычно приводиться в справочных данных конкретных магнитопроводоа [], а для кольцевых магнитопроводов может быть легко рассчитан: AL = μ0μэффSэфф/lэфф, где μ0= 1,257·10−3 мкГн/мм – абсолютная магнитная проницаемость вакуума, μэфф – эффективная начальная магнитная проницаемость материала магнитопровода, Sэфф – эффективная площадь сечения магнитопровода в мм2, lэфф – эффективная длина магнитопровода в мм.

Зная величину АL нетрудно определить число витков катушки для получения необходимой индуктивности:.

Эффективное сечение и длина магнитопровода несколько меньше определяемых по его геометрическим параметрам и обычно приводятся в справочной литературе. В табл. 36 в первых пяти столбцах, приведены геометрические размеры, эффективные сечение Sэфф и длин lэфф для ферритовых колец стандартного ряда с внешним диаметром D от 6 до 50 мм, внутренним d и высотой h [].

В этой же таблице приведены расчетные значения площади окна магнитопроводов Sокн, периметра сечения р и коэффициента индуктивности AL для μэфф= 50. Данные позволяют рассчитать индуктивность любой катушки, намотанной на кольцевом магнитопроводе с табличными геометрическими размерами. Если μэфф используемого кольца отличается от 50, значение АL необходимо пропорционально изменить, например, для μэфф = 2000коэффициент АL следует увеличить в 40 раз. Следует иметь ввиду, что значения μэфф , Sэфф и lэфф – определяются с большой погрешностью, и в справочниках для кольцевых магнитороводов указан обычно двукратный разброс значений АL []. Поэтому величины AL, взятые из табл. 1, следует принимать за ориентировочные и уточнять их при необходимости более точного расчета по результатам эксперимента.

Для этого следует намотать на магнитопроводе пробную катушку, например, из десяти витков и измерить ее индуктивность Lпр. Здесь себя хорошо зарекомендовал прибор, описанный в []. Разделив Lпр на 100 = 102, определим значение АL. Расчетное значение N следует увеличить на несколько витков (до N1), по результату измерения L1 уточнить необходимое число витков и отмотать лишние витки.

Описанным выше образом можно рассчитать индуктивность катушки или необходимое число витков. Однако, как только речь заходит о дросселях для импульсных источников питания, сразу возникает вопрос, какой ток может выдержать дроссель без насыщения магнитопровода?

Магнитная индукция В в магнитопроводе при токе I может быть рассчитана по формуле В = μ0μэффIN/lэфф.

Максимально допустимая индукция Вmax для материалов магнитопроводов приводится в справочных данных и лежит в пределах 0,25…0,4 Тл. Из этой формулы несложно получить выражение для максимального тока дросселя: Imax = Bmax lэфф/(μ0μэффN).

Если в нее подставить формулу для определения числа витков по заданной индуктивности, получим 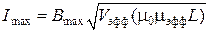, где Vэфф = Sэффlэфф– эффективный объем магнитопровода. Нетрудно видеть, что чем выше μэфф, тем меньший ток может пропустить дроссель при тех же геометрических размерах магнитопровода и заданной индуктивности. Более или менее приемлемые результаты при изготовлении дросселей для ИВЭП получаются при μэфф= 30…50. Именно поэтому в табл. 36 значение коэффициента АL приведено для μэфф = 50. В этой же таблице приведено максимальное значение тока Imax через дроссель с одним витком при Вmax= 0,3Тл. Для определения допустимого тока реального дросселя достаточно табличное значение Imaxразделить на число витков N.

Однако в радиолюбительской практике более доступны кольцевые магнитопроводы с большими значениями эффективной магнитной проницаемости μэфф= 1000…4000. Понизить эффективную магнитную проницаемость таких магнитопроводов можно введением зазора, при этом

μэфф = μнач /(1+ μначΔэфф/lэфф), где μнач – начальная магнитная проницаемость материала магнитопровода, Δэфф – эффективная ширина зазора. При реальной ширине зазора μэфф ≡ lэфф / Δэфф. Для того, чтобы снизить μэфф примерно до 50…100 (это значение исходя из опыта расчета и изготовления дросселей близко к оптимальному), эффективная ширина зазора должна составлять Δэфф = lэфф /(50…100) независимо от начальной магнитной проницаемости магнитопровода.

Если в вышеприведенную формулу для расчета АL подставить значение μэфф для магнитопровода с зазором, получим АL = μ0Sэфф /Δэфф .

Еще более простой получается формула для максимального тока через дроссель Imax = BmaxΔэфф /(m0N) ≡ 240Δэфф /N (для Вmax = 0,3 Тл), т.е. допустимый ток определяется только эффективным зазором и числом витков.

Таблица 36

D, мм   d, мм   h, мм   lэфф, мм   Sэфф,мм2   Sокн,мм2   P, мм   Без зазора (μэфф=50) АL, мкГн с зазором, мм   I2L, A2 мкГн с зазором, мм
0,25 0,5 1.5
АL, мкГн   Imax,A (N=1) 0,25   0,5     1,5   нас. зап. нас. зап. нас. зап. нас. зап.
  2,5   1,8   11,8   2,96   4,9   7,1   0,016   56,28   0,03   0,02   0,012   0,01   30,65   0,3487   46,8   0,229   67,2   0,1591   81,3   0,1314  
    2.4   13,1   3,53   7,1   7,8   0,017   62,34   0,03   0,02   0,013   0,011   37,72   0,8357   58.1   0,543     0,3751     0,3089  
    1.5   16,4   2,19       0,008   78,33   0,02   0,01   0,009   0,008   21,37   1,7945   32,1   1,195   45,5   0,8421   54,85   0,6989  
      16,4   2,92       0,011   78,33   0,03   0,02   0,012   0,01   30,09   2,2654   45,8   1,487   65,8   1 ,0362   79,58   0,8564  
7,5     2,2   14,4   4,62   7,1   8,9   0,02   68,69   0,04   0,02   0,016   0,013   51,48   1,0488   80.3   0,672     0,4597   143,2   0,3769  
    2,5   17,4   4,9       0,018   83,1   0,04   0,03   0,017   0,014   54,79   3,5035   85,6   2,243     1,5324   152,8   1,2561  
      22,9   4,44       0,012   109,5   0,04   0,02   0,016   0,013   49,64   16,071   77,5   10,29     7,0299   138,4   5,7624  
      19,2   8,4       0,028   91.6   0,06   0,04   0,026   0,021     5,5315     3,441     2,2916   303,7   1,8568  
      24,1   3,91       0,01   114,9   0,03   0,02   0,015   0,012   42,12   14,688     9,515   94,3   6,5635   114,5   5,4021  
      24,1   5,87       0,015   114,9   0,05   0,03   0,02   0,016   67,73   20,588     13,04     8,8311   193,4   7,21  
    4,5   24,1   8,81       0,023   114,9   0,06   0,04   0,026^   0,021   109,2   28,765     17,75     11,734   331,5   9,4738  
      24,1   9,63       0,025   114,9   0,07   0,04   0,028   0,022   121,6   30,866     18,91     12,41   375,8   9,9858  
    5,5   23,6   18,1       0,048   112,5   0,12   0,07   0,047   0,037   241,6   26,376     15,77     10,098   794,2   8,0238  
    4,5   26,1         0,031   124,7   0,09   0,06   0,036   0,029   166,5   40,889     24,88     16.221   523,3   13,008  
      30,6   5,92       0,012   145,9   0,05   0,03   0,02   0,016   68,31   65,624     41,58     28,148     22,981  
      29,7   4,97       0,011   141,6   0,04   0,02   0,016   0,013   58,93   85,886   93,9   53,9     36,18   171,9   29,425  
  5,5   5   25,7   17,6       0,043   122,7   0,12   0,07   0,046   0,036   233,5   37.775     22,65     14,542   762,3   11,571  
    4,5   28,8   18,9       0,041   137,4   0,13   0,08   0,049   0,039   252,6   57,175     34,19     21,89   830,2   17,393  
    2,5   23,2   12,8       0,035   110,9   0,09   0,05   0,034   0,027   169,2   7,7536     4,662     3,0017   548,3   2,3921  
      34,9   23,1       0,042   166,4   0.15   0,09   0,057   0,045   315,1   215,87     127,8     80,981     63,984  
    4,5   39,4   13,3       0,021   187,9   0,09   0,06   0,037   0,03   170,1   322,31     196,1     127,86   534.6   102,54  
  5,5   2,3   28,8   11,9       0,026   137,6   0,08   0,05   0,032   0,026   155,4   26,082     15,76     10,205     8,1551  
  8,2     36,8   22,2       0,038   175,4   0,15   0,09   0,056   0,044   300,8   230,73     137,1     87,153     68,993  
    5   39,2   21,6       0,035   187,1   0,14   0,09   0,055   0,043   292,4   327,57     194,9     124,1   973,9   98,328  
      49,7   23,9       0,03   237,4   0,15   0,09   0,052   0,04   346,4   1973,2         694,75     538,66  
      43,6         0,035   207,9   0,16   0,09   0,059   0,047   328,2   548,98         205,94     162,71  
    7,5   43,6         0,052   207,9   0,23   0,13   0,082   5:064     789,86     458,3     283,99     221,62  
      48,1   15,4       0,02   229,8   0,11   0,06   0,042   0,033   200,8   765,79     463,1       641,2   239,81  
      48,1   23,5       0,031   229,8   0,15   0,09   0,058   0,046   320,8   1112,8     658,8     417,43     329,82  
    7,5   48,1   28,9       0,038   229,8   0.19   0,11   0,068   0,053   405,4   1333,2     779,3     486,94     381,79  
      46,9   24,2       0,032     0,16   0,09   0,06   0,047     808,11     478,5     303,14     239,52  
    6,5   45,4         0,051   216,8   0,23   0,14   0,084   0,066   527,5   812,22     471,3     292,03     227,89  
      53,2   37,3       0,044     0,24   0,14   0,085   0,066   531,2   1696,1     984,2     609,81     475,88  
      53,2   55,9       0,066     0,34   0,19   0,118   0,091   824,7           849,32     654,61  
    7,5   57,8   36,7       0,04   275,9   0,23   0,13   0,083   0,065   522,6   4074,1         1464,8     1143,1  
      65,6   34,1       0,033   313,3   0,22   0,13   0,079   0,062   482,7   4941,4         1790,3     1400,3  
      65,6   52,6       0,05   313,3   0,32   0,18   0,112   0,087   771,8   7339,4             1970,7  
  18,5     74,4   42,8       0,036   355,2   0,27   0,15   0,095   0,074   615,4           3870,8     3010,6  
  18,5     74,4   85,6       0,072   355,2   0,5   0,28   0,166   0,126             6759,4     5128,6  
      69,7   61,5       0,055   332,6   0,37   0,21   0,128   0,099             2920,6     2246,9  
      69,7   92,3       0,083   332,6   0,54   0,3   0,18   0,137             4090,3     3105,7  
      78,8   35,3       0,028   375.9   0,22   0,13   0,082   0,064   499,7           4524,6      
      78,8         0,042   375,9   0,33   0.19   0,113   0,087   777,8               4848,8  
        48,2       0,032   448,9   0,3   0,17   0,105   0,082   698,8                
      87,1   48,1       0,035   415,8   0,29   0,17   0,103   0,079   704,9           5690,4     4394,3  
    7,5   87,1   72,1       0,052   415.8   0,43   0,24   0,146   0,112             8121,8     6215,4  
      96,3   93,9       0,061   459,6   0,55   0,31   0,183   0,139                  
    7,5   98,4   55,2       0,035   469,9   0,34   0,19   0,118   0,091   810,2                
      98,4   81,1       0,052   469,9   0,48   0,27   0,162   0.123                  
        66,7       0,038   527,3   0,4   0,23   0,138   0,106                  
        97,8       0,056   527,3   0,57   0,32   0,189   0,144                  
        72,1       0,042   519,7   0,43   0,24   0,144   0,11                  
              0.062   519,7   0,63   0,35   0,206   0,156                  
        97,9       0,051   574,5   0,58   0,32   0,191   0,145                  

 

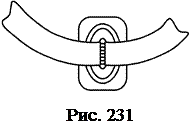Почти все приведенные выше формулы уже были опубликованы в журнале «Схемотехника» [4 найти первоисточник], однако ни в одной из известных автору статьи публикаций не отмечено, что эффективная ширина зазора, которую надо применять в расчетах, меньше геометрической. Это различие возникает из-за того, что магнитное поле, существующее рядом с зазором (рис. 231), шунтирует зазор и уменьшает его эффективную ширину. Для того, чтобы рассчитать влияние этого поля, можно обратиться к аналогии между магнитным и электрическим полями. Воспользуемся формулой для емкости конденсатора из двух цилиндров с близко расположенными торцами []:

С = D2/(16d)+D/(8π)×{1+ln[8πD(d+b)/d2]+b/d×ln(1+d/b)},

где С – емкость конденсатора в сантиметрах, D – диаметр цилиндров, b – их высота, d – зазор между их торцами.

Нетрудно заметить, что первое слагаемое соответствует емкости зазора между цилиндрами, а второе – емкости, вносимой боковыми поверхностями цилиндров. Будем считать, что высота цилиндров равна их удвоенному диаметру b = 2D. Это означает, что мы учтем только емкость ближайшей к зазору части боковой поверхности цилиндров, пренебрегая дальней. Расчеты при длине цилиндров в 3 или 4 диаметра дают практически тот же результат.

Для того, чтобы в дальнейшем перейти от емкости между цилиндрами к емкости между прямоугольными брусками (а это по форме ближе к сечению ферритового кольца), будем считать, что емкость, вносимая боковыми поверхностями, пропорциональна периметру зазора, и выразим в этой формуле диаметр цилиндров через периметра р их кругового сечения:, высота цилиндров .

Если в формулу для емкости подставить эти выражения, можно определить из нее отношение полной емкости к емкости между торцами в функции от отношения зазора к периметру цилиндров 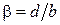. Формула эта, однако, получается довольно громоздкой и неудобной для применения.

Обозначим буквой αотношение эффективного зазора, обеспечивающего без емкости боковых поверхностей ту же емкость, что и емкость между торцами с учетом емкости боковых поверхностей к геометрическому. На рис. 232 приведена расчетная зависимость α от β. Из подобия уравнений, описывающих электрическое и магнитное поле, следует, что аналогично выглядит и зависимость отношения эффективного магнитного зазора к геометрическому от отношения геометрического магнитного зазора к периметру.

Из графика на рис. 232 следует, что эффективная ширина зазора может существенно отличаться от геометрической. В реальном диапазоне β составляет от 0,01 до 0,1 эффективная ширина зазора меньше геометрической в 1,26…2,66 раза.

В табл. 336 приведены значения АL для кольцевых магнитопроводов с четырьмя различными зазорами, рассчитанные с учетом отличия эффективного зазора от геометрического.

Вышесказанное позволяет сделать вывод, что необходимые число витков и зазор практически не зависят от начальной магнитной проницаемости материала магнитопровода, и поэтому можно применить ферриты с любой проницаемостью, большей 600. Для любого имеющегося кольца с табличным зазором по значению АL нетрудно вычислить индуктивность или необходимое число витков и рассчитав , по графику (рис. 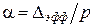232) определить значение и 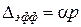. По найденному значению 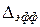и приведенной ранее формуле можно найти максимальный ток, не вызывающий насыщения сердечника.

Однако существует еще одно обстоятельство, влияющее на выбор магниторовода – возможность намотки на него требуемого числа витков проводом соответствующего сечения. Необходимая площадь окна кольца составляет 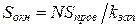, где – сечение провода, а 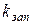– коэффициент заполнения окна. Расчет производят по формуле , где j – допустимая плотность тока. Типовое значение 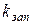по меди составляет 0,3, а для j при начальном расчете принимают значение 2,5 А/мм2.

Подставив в формулу для расчета площади окна выражения для N и AL, получим следующую формулу:

.

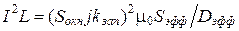Подобное выражение можно получить и из формулы для максимального тока, который можно пропустить через дроссель без насыщения сердечника:

.

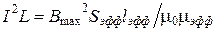Однозначного расчета конструктивных параметров дросселя по заданным индуктивности и току не существует. Однако при подборе кольца и определении данных обмотки могут помочь последние восемь колонок табл. 36. В них приведены максимальные значения произведения 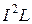по насыщению и по заполнению, рассчитанные для Тл, , 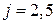А/мм2 и четырех значений зазора.

Подбор колец и расчет конструктивных параметров дросселей продемонстрируем на двух примерах.

Пусть необходим дроссель индуктивностью 22 мкГн на рабочий ток 1,2 А. Для него значение 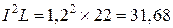. Среди колец минимального диаметра первым почти подходит кольцо К10×6×4,5. При введении в него зазора 0,25 мм имеем возможность намотать дроссель с большим запасом по току (табл. 36, колонка «нас.»), но с некоторым превышением плотности тока относительно 2,5 А/мм2 (колонка «зап.»).

Определим параметры дросселя при зазоре 0,25 мм. Для него коэффициент индуктивности по табл. 36 составит 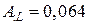, необходимое число
витков 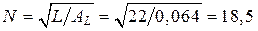(округляем до 19), допустимый ток А.

Для А при 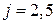А/мм2 необходимо провод сечением

мм2.

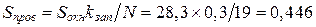При коэффициенте заполнения необходимая площадь окна составит мм2. Площадь окна по табл. 36 составляет 28,3 мм2, что несколько меньше. Необходимом за счет увеличения плотности тока уменьшить сечение провода до мм2.

Плотность тока составит 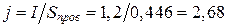А/мм2, что вполне допустимо. Диметр провода указанного сечения (по меди) можно рассчитать по формуле:

мм.

Пусть необходим дроссель 88 мкГн на ток 1,25 А. Для него I2L = 137,5. Дроссель можно намотать на кольце К12×6×4,5 с тем же зазором, при этом насыщение магнитопровода происходить не будет, но плотность тока существенно превысит норму. Поэтому необходимо перейти к кольцу большего размера. В распоряжении автора были кольца К12×8×3 и феррита М4000НМ. На одном кольце невозможно намотать необходимы дроссель, ни по насыщению сердечника, ни по заполнению окна. Можно сложить два кольца вместе. В этом случае эффективное сечение магнитопровода увеличивается в два раза, а допустимые значение I2L вырастут по насыщению несколько более, а по заполнению несколько менее, чем в два раза. Поэтому необходимый дроссель при геометрическом зазоре 0.25 мм можно намотать с запасом по току насыщения и с небольшим превышением плотности тока.

Только табличными сведениями теперь не обойтись, необходим полный расчет. Для двух колец периметр сечения 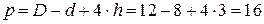мм, при зазоре 0,25 мм .

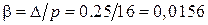По графику на рис. 262 находим α = 0,73, откуда эффективный зазор 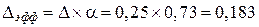мм.

Найденное значение .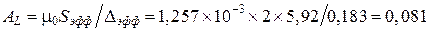

Необходимое число витков 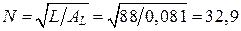округляя в большую сторону до 33 витков. Максимальный ток через дроссель 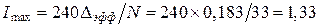А.

Максимальное сечение провода мм2, что соответствует плотности тока 1,25/0,457 = 2,74 А/мм2. Сечению 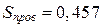мм2 соответствует диаметр мм.

Иногда удобнее ввести два одинаковых зазора. В этом случае табличное значение АL для половинного зазора следует уменьшить в два раза, а табличное значение I2L для половинного зазора – удвоить.

Технология введения зазора такова. Небольшое кольцо перед намоткой разломить на две части, надпилив его надфилем, лучше алмазным. Половинки склеивают между собой эпоксидным клеем с наполнителем, в качестве которого удобно использовать тальк. При склеивании в один из зазоров или в оба на часть глубины вводят прокладку из гетинакса, текстолита или нескольких слоев бумаги. Можно считать, что толщина одного листа бумаги для ксероксов и лазерных принтеров составляет 0,1 мм. Для сохранения формы кольца в процессе полимеризации клея оно должно лежать на обрезке органического стекла, от которого затем легко отделяется при изгибе этого обрезка. Перед намоткой острые грани колец следует тщательно скруглить небольшим наждачным камнем.

У большого кольца зазор можно также выполнить ножовкой с алмазным полотном, однако его ширина при этом однозначно определяется толщиной полотна. В такой зазор для сохранения прочности кольца следует вклеить прокладку их жесткого диэлектрика.

Для экспериментальной проверки тока насыщения дросселей в[120] на микросхеме DD1собран генератор импульсов положительной полярности длительностью, регулируемой в пределах 10...300 мкс с периодом повторения около 10 мс. Импульсы с его выхода поданы на затвор мощного, но низковольтного и относительно недорогого полевого транзистора VТ2.Транзистор открывается и через проверяемую катушку индуктивности L1 начинает течь линейно нарастающий ток. Когда импульс заканчивается, накопленная энергия передается через диод VD2в нагрузку, которой служат стабилитроны VD3и VD4. Напряжение с резистора R7, пропорциональное току через катушку L1, подается на осциллограф. Для синхронизации осциллографа лучше использовать сигнал с выхода DD1.4. Если ток превысит 6 А, откроется транзистор VТ1и оборвет формирование импульса. Пока сердечник катушки не входит в насыщение, зависимость тока от времени, как указывалось выше, носит линейный характер. При плавном увеличении длительности импульсов и подходе максимального тока через дроссель к току насыщения на экране осциллографа хорошо видно резкое отклонение зависимости от линейной. Источник напряжением 20 В должен допускать выходной ток не менее 1 А. Для упрощения пользования приставкой можно цепь +6 В питать от цепи +20 В через микросхемный стабилизатор КР145ЕН5Б(Г), либо КР1157ЕН6 с любым суффиксами (7806 или 78L06).

Экспериментальная проверка изготовленных дросселей подтвердила точность расчетанеобходимого числа витков и тока насыщения порядка ±10 %, что можно считать неплохим результатом, учитывая ошибки установки ширины зазора и множество допущений при выводе формул.