Теорема существования и единственности
Лекция 3
Известно, какую большую роль в алгебре играют теоремы, отвечающие на вопрос о том, сколько решений имеет та или другая система алгебраических уравнений. Такова, например, основная теорема алгебры, утверждающая, что многочлен n-й степени всегда имеет ровно n корней (считая с их кратностями). Точно так же в теории дифференциальных уравнений важным теоретическим вопросом является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и потому приходится ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности.
Теорема. Пусть
 (1)
(1)
— дифференциальное уравнение. Будем предполагать, что функция  задана на некотором открытом множестве
задана на некотором открытом множестве  плоскости
плоскости  переменных
переменных  . Относительно функции
. Относительно функции  будем предполагать, что она сама и ее частная производная
будем предполагать, что она сама и ее частная производная  являются непрерывными функциями на всем открытом множестве
являются непрерывными функциями на всем открытом множестве  . Теорема утверждает, что:
. Теорема утверждает, что:
1) для всякой точки  множества
множества  найдется решение
найдется решение  уравнения (1), удовлетворяющее условию
уравнения (1), удовлетворяющее условию
 ; (2)
; (2)
2) если два решения  и
и  уравнения (1) совпадают хотя бы для одного значения
уравнения (1) совпадают хотя бы для одного значения  , т.е. если
, т.е. если  , то решения эти тождественно равны для всех тех значений переменной
, то решения эти тождественно равны для всех тех значений переменной  , для которых они оба определены.
, для которых они оба определены.
Числа  называются начальными значениями для решения
называются начальными значениями для решения  , а соотношение (2) — начальным условием для этого решения. Говорят также, что решение
, а соотношение (2) — начальным условием для этого решения. Говорят также, что решение  удовлетворяет начальному условию(2) или же что оно имеет начальные значения
удовлетворяет начальному условию(2) или же что оно имеет начальные значения  . Утверждение, что решение
. Утверждение, что решение  удовлетворяет начальному условию (2) (или имеет начальные значения
удовлетворяет начальному условию (2) (или имеет начальные значения  ), предполагает, что интервал
), предполагает, что интервал  определения решения
определения решения  содержит точку
содержит точку  .
.
Таким образом, теорема утверждает, что координаты любой точки  множества
множества  являются начальными значениями для некоторого решения уравнения (1) и что два решения с общими начальными значениями совпадают.
являются начальными значениями для некоторого решения уравнения (1) и что два решения с общими начальными значениями совпадают.
Геометрическое содержание теоремы заключается в том, что через каждую точку  множества
множества  проходит одна и только одна интегральная кривая уравнения (1).
проходит одна и только одна интегральная кривая уравнения (1).
Говоря, что через каждую точку  множества
множества  проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (1) называется функция
проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (1) называется функция  , заданная на вполне определенном интервале
, заданная на вполне определенном интервале  . Наряду с этой функцией может существовать функция
. Наряду с этой функцией может существовать функция  , также удовлетворяющая уравнению (1) и имеющая те же начальные значения
, также удовлетворяющая уравнению (1) и имеющая те же начальные значения  , но заданная на другом интервале
, но заданная на другом интервале  . Вторая часть теоремы утверждает лишь, что функции
. Вторая часть теоремы утверждает лишь, что функции  и
и  совпадают там, где они обе определены, но вовсе не утверждает, что интервалы их определения
совпадают там, где они обе определены, но вовсе не утверждает, что интервалы их определения  и
и  одинаковы.
одинаковы.
Если один из интервалов, например  , полностью содержит другой, то мы будем говорить, что решение
, полностью содержит другой, то мы будем говорить, что решение  , заданное на интервале
, заданное на интервале  , является продолжением решения
, является продолжением решения  . Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Можно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение о том, что через каждую точку
. Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Можно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение о том, что через каждую точку  проходит единственная интегральная кривая, становится точным.
проходит единственная интегральная кривая, становится точным.
Каждое решение  уравнения (1) мы интерпретировали геометрически в виде графика функции
уравнения (1) мы интерпретировали геометрически в виде графика функции  . Дадим теперь геометрическую интерпретацию самого уравнения (1). Через каждую точку
. Дадим теперь геометрическую интерпретацию самого уравнения (1). Через каждую точку  множества
множества  проведем прямую
проведем прямую  с угловым коэффициентом
с угловым коэффициентом  . Мы получаем поле направлений, соответствующее уравнению (1), что и дает геометрическую интерпретацию этого уравнения.
. Мы получаем поле направлений, соответствующее уравнению (1), что и дает геометрическую интерпретацию этого уравнения.
Связь между геометрической интерпретацией уравнения и геометрической интерпретацией его решений заключается в том, что любая интегральная кривая  в каждой своей точке
в каждой своей точке  касается прямой
касается прямой  .
.
Пример. Для того, чтобы проиллюстрировать значение теоремы (в данном случае — второй ее части), решим дифференциальное уравнение
 , (3)
, (3)
где  — действительное число. Здесь
— действительное число. Здесь  , так что функция
, так что функция  в действительности зависит лишь от переменной
в действительности зависит лишь от переменной 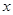 . Множество точек, на котором определена функция
. Множество точек, на котором определена функция  , в данном случае совпадает со всей плоскостью
, в данном случае совпадает со всей плоскостью  . Как сама функция
. Как сама функция  , так и ее частная производная
, так и ее частная производная  являются непрерывными функциями переменных
являются непрерывными функциями переменных  во всей плоскости
во всей плоскости  . Таким образом, теорема к уравнению (3) применима. Непосредственной подстановкой в уравнение (3) проверяется, что каждая функция
. Таким образом, теорема к уравнению (3) применима. Непосредственной подстановкой в уравнение (3) проверяется, что каждая функция
 , (4)
, (4)
где  — произвольное действительное число, является решением уравнения (3). Решение это непродолжаемо, так как оно задано уже на всей прямой
— произвольное действительное число, является решением уравнения (3). Решение это непродолжаемо, так как оно задано уже на всей прямой  . Покажем, что, придавая всевозможные значения числу
. Покажем, что, придавая всевозможные значения числу  , мы получим все решения уравнения (3). Пусть
, мы получим все решения уравнения (3). Пусть  — произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа
— произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа  мы имеем
мы имеем  . Пусть
. Пусть  — некоторая точка интервала существования решения
— некоторая точка интервала существования решения  и
и  . Положим
. Положим  . Тогда решения
. Тогда решения  и
и  уравнения (3) имеют одинаковые начальные значения
уравнения (3) имеют одинаковые начальные значения  и потому в силу второй части теоремы совпадают. Таким образом, формула (4) исчерпывает совокупность всех решений дифференциального уравнения (3).
и потому в силу второй части теоремы совпадают. Таким образом, формула (4) исчерпывает совокупность всех решений дифференциального уравнения (3).
Доказательство теоремы проводится методом последовательных приближений (или же, другими словами, методом сжимающих отображений).
Основные идеи доказательства. Первым шагом при доказательстве теоремы методом последовательных приближений является переход от дифференциального уравнения к интегральному, который мы сформулируем в виде отдельного предложения.
А) Пусть  — произвольное решение уравнения (1), определенное на интервале
— произвольное решение уравнения (1), определенное на интервале  , так что выполнено тождество
, так что выполнено тождество
 , (5)
, (5)
и пусть
 (6)
(6)
— некоторое начальное условие, которому это решение удовлетворяет. Оказывается, что тогда для функции  на всем интервале
на всем интервале  выполнено интегральное тождество
выполнено интегральное тождество
 . (7)
. (7)
Обратно, если для некоторой непрерывной функции  на интервале
на интервале  выполнено тождество (7), то функция
выполнено тождество (7), то функция  дифференцируема, является решением уравнения (1) и удовлетворяет начальному условию (6). Кратко говоря, интегральное уравнение (7) эквивалентно дифференциальному уравнению (5) вместе с начальным условием (6).
дифференцируема, является решением уравнения (1) и удовлетворяет начальному условию (6). Кратко говоря, интегральное уравнение (7) эквивалентно дифференциальному уравнению (5) вместе с начальным условием (6).
Докажем это. Допустим сначала, что выполнено соотношение (7). Заменяя в нем переменную  ее значением
ее значением  , получаем:
, получаем:  . Таким образом, из (7) вытекает (6). Далее, правая часть тождества (7) очевидно дифференцируема по
. Таким образом, из (7) вытекает (6). Далее, правая часть тождества (7) очевидно дифференцируема по  , а потому левая его часть также дифференцируема по
, а потому левая его часть также дифференцируема по  . В результате дифференцирования тождества (7), получаем тождество (5).
. В результате дифференцирования тождества (7), получаем тождество (5).
Допустим теперь, что выполнены соотношения (5) и (6). Интегрируя соотношение (5) в пределах от  до
до  , получаем:
, получаем:  . В силу соотношения (6) из последнего равенства получаем (7). Таким образом, предложение А) доказано.
. В силу соотношения (6) из последнего равенства получаем (7). Таким образом, предложение А) доказано.
Введем теперь некоторые обозначения, используемые далее при доказательстве теоремы.
Б) Пусть  — такая непрерывная функция, определенная на некотором отрезке
— такая непрерывная функция, определенная на некотором отрезке  , что ее график целиком расположен в открытом множестве
, что ее график целиком расположен в открытом множестве  , и
, и  — некоторая точка отрезка
— некоторая точка отрезка  . Тогда, пользуясь правой частью тождества (7), можно функции
. Тогда, пользуясь правой частью тождества (7), можно функции  поставить в соответствие функцию
поставить в соответствие функцию  , определенную также на отрезке
, определенную также на отрезке  , при помощи равенства
, при помощи равенства
 (8)
(8)
(график функции  , конечно, уже может не проходить в множестве
, конечно, уже может не проходить в множестве  ). Таким образом, правую часть тождества (7) можно рассматривать как оператор, ставящий в соответствие функции
). Таким образом, правую часть тождества (7) можно рассматривать как оператор, ставящий в соответствие функции 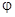 функцию
функцию  . Обозначая этот оператор одной буквой
. Обозначая этот оператор одной буквой  , мы запишем соотношение (8) в виде формулы
, мы запишем соотношение (8) в виде формулы
 . (9)
. (9)
Пользуясь оператором  , интегральное уравнение (7) можно записать в виде
, интегральное уравнение (7) можно записать в виде
 . (10)
. (10)
В) Пусть  — некоторая непрерывная функция, определенная на отрезке
— некоторая непрерывная функция, определенная на отрезке  . Нормой
. Нормой  этой функции называется максимум ее модуля:
этой функции называется максимум ее модуля:  . Если
. Если  и
и  — две непрерывные функции, заданные на отрезке
— две непрерывные функции, заданные на отрезке  , то норма их разности
, то норма их разности  является неотрицательным числом, оценивающим, насколько сильно отличаются эти функции друг от друга. Если число
является неотрицательным числом, оценивающим, насколько сильно отличаются эти функции друг от друга. Если число  мало, то функции
мало, то функции  и
и  близки друг к другу. Равенство
близки друг к другу. Равенство  имеет место тогда и только тогда, когда функции
имеет место тогда и только тогда, когда функции  и
и  тождественно совпадают. Пользуясь понятием нормы, можно сформулировать известное вам из курса матанализа условие равномерной сходимости последовательности непрерывных функций. Пусть
тождественно совпадают. Пользуясь понятием нормы, можно сформулировать известное вам из курса матанализа условие равномерной сходимости последовательности непрерывных функций. Пусть
 (11)
(11)
— последовательность непрерывных функций, заданных на отрезке  . Последовательность (11) равномерно сходится к функции
. Последовательность (11) равномерно сходится к функции 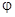 , определенной на том же отрезке
, определенной на том же отрезке  , если
, если  . Для того, чтобы последовательность (11) равномерно сходилась, достаточно, чтобы имели место равенства
. Для того, чтобы последовательность (11) равномерно сходилась, достаточно, чтобы имели место равенства  , где числа
, где числа  образуют сходящийся ряд.
образуют сходящийся ряд.
Прежде чем перейти к детальному проведению доказательства теоремы, изложим кратко суть метода последовательных приближений, применяемого для решения уравнения (10). Строится последовательность
 (12)
(12)
непрерывных функций, определенных на некотором отрезке  , который содержит внутри себя точку
, который содержит внутри себя точку  . Каждая функция последовательности (12) определяется через предыдущую при помощи равенства
. Каждая функция последовательности (12) определяется через предыдущую при помощи равенства
 (13)
(13)
Если график функции  проходит в множестве
проходит в множестве  , то функция
, то функция  равенством (13) определяется, но для того, чтобы могла быть определена следующая функция
равенством (13) определяется, но для того, чтобы могла быть определена следующая функция  , нужно, чтобы и график функции
, нужно, чтобы и график функции  проходил в множестве
проходил в множестве  . Этого, как мы покажем, удается достичь, выбрав отрезок
. Этого, как мы покажем, удается достичь, выбрав отрезок  достаточно коротким. Далее, также за счет уменьшения длины отрезка
достаточно коротким. Далее, также за счет уменьшения длины отрезка  , можно достичь того, чтобы для последовательности (12) выполнялись неравенства
, можно достичь того, чтобы для последовательности (12) выполнялись неравенства
 (14)
(14)
где  . Из неравенств (14) следуют неравенства
. Из неравенств (14) следуют неравенства
 ,
,
и, таким образом, последовательность (12) равномерно сходится (см. предположение В)). Далее уже легко устанавливается, что предел 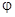 последовательности (12) удовлетворяет уравнению (10).
последовательности (12) удовлетворяет уравнению (10).
Ту же конструкцию можно описать несколько иным способом — в форме метода сжимающих отображений. Выберем некоторое семейство  функций, заданных на отрезке
функций, заданных на отрезке  (причем
(причем  ), так, чтобы графики этих функций проходили в множестве
), так, чтобы графики этих функций проходили в множестве  . Допустим еще, что в отношении оператора
. Допустим еще, что в отношении оператора  семейство
семейство  удовлетворяет следующим двум условиям: 1) применяя оператор
удовлетворяет следующим двум условиям: 1) применяя оператор  к любой функции семейства
к любой функции семейства  , мы вновь получаем функцию семейства
, мы вновь получаем функцию семейства  ; 2) существует такое число
; 2) существует такое число 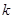 ,
,  , что для двух произвольных функций
, что для двух произвольных функций  и
и  семейства
семейства  выполнено неравенство
выполнено неравенство  . В этом смысле отображение
. В этом смысле отображение  является сжимающим.
является сжимающим.
Легко видеть, что если для семейства  выполнены сформулированные условия, то, исходя из произвольной его функции
выполнены сформулированные условия, то, исходя из произвольной его функции  , мы по индуктивной формуле (13) получим бесконечную последовательность (12), удовлетворяющую условию (14), и, как мы отмечали ранее, равномерно сходящуюся к решению
, мы по индуктивной формуле (13) получим бесконечную последовательность (12), удовлетворяющую условию (14), и, как мы отмечали ранее, равномерно сходящуюся к решению 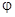 уравнения (10).
уравнения (10).
Теперь перейдем к доказательству теоремы на основе изложенных соображений.
Доказательство теоремы существования и единственности. Начальные значения  и
и 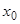 искомого решения уравнения (1) являются координатами точки
искомого решения уравнения (1) являются координатами точки  , лежащей в множестве
, лежащей в множестве  .Выберем прежде всего какой-либо прямоугольник
.Выберем прежде всего какой-либо прямоугольник  с центром в точке
с центром в точке  со сторонами, параллельными осям, целиком вместе со своей границей содержащийся в множестве
со сторонами, параллельными осям, целиком вместе со своей границей содержащийся в множестве  . Длину горизонтальной (параллельной оси
. Длину горизонтальной (параллельной оси  ) стороны прямоугольника
) стороны прямоугольника  обозначим через
обозначим через  , а длину вертикальной стороны — через
, а длину вертикальной стороны — через  . Таким образом, точка
. Таким образом, точка  тогда и только тогда принадлежит прямоугольнику
тогда и только тогда принадлежит прямоугольнику  , когда выполнены неравенства
, когда выполнены неравенства
 . (15)
. (15)
Так как прямоугольник  есть замкнутое множество, содержащееся в
есть замкнутое множество, содержащееся в  , то непрерывные на нем функции
, то непрерывные на нем функции  и
и  ограничены, и потому существуют такие положительные числа
ограничены, и потому существуют такие положительные числа  и
и  , что для
, что для  и
и 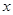 , удовлетворяющих условиям (15), выполнены неравенства
, удовлетворяющих условиям (15), выполнены неравенства
 . (16)
. (16)
Наряду с прямоугольником  будем рассматривать более «узкий» прямоугольник
будем рассматривать более «узкий» прямоугольник  , определяемый неравенствами
, определяемый неравенствами  , где
, где
 (17)
(17)
. Более точно число  определим далее. Обозначим через
определим далее. Обозначим через  семейство всех непрерывных функций, заданных на отрезке
семейство всех непрерывных функций, заданных на отрезке  , графики которых проходят в прямоугольнике
, графики которых проходят в прямоугольнике  . Таким образом, функция
. Таким образом, функция 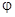 , определенная на отрезке
, определенная на отрезке  , тогда и только тогда принадлежит семейству
, тогда и только тогда принадлежит семейству  , когда для любого
, когда для любого  , принадлежащего этому отрезку, выполнено неравенство
, принадлежащего этому отрезку, выполнено неравенство
 . (18)
. (18)
Постараемся теперь выбрать число  таким образом, чтобы были выполнены следующие два условия:
таким образом, чтобы были выполнены следующие два условия:
а) Если функция 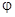 принадлежит семейству
принадлежит семейству  , то функция
, то функция  (см. (8), (9)) также принадлежит семейству
(см. (8), (9)) также принадлежит семейству  .
.
б) Существует такое число  , что для любых двух функций
, что для любых двух функций  и
и  семейства
семейства  имеет место неравенство
имеет место неравенство
 . (19)
. (19)
Рассмотрим условие а). Для того, чтобы функция  принадлежала семейству
принадлежала семейству  , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при  было выполнено неравенство
было выполнено неравенство  . В силу (8) и (16) мы имеем
. В силу (8) и (16) мы имеем  . Из этого видно, что при
. Из этого видно, что при
 (20)
(20)
условие а) выполнено.
Рассмотрим теперь условие б). Мы имеем:
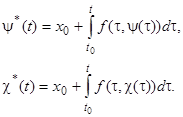
Вычитая второе равенство из первого, получаем
 . (21)
. (21)
Оценим теперь последнее подынтегральное выражение, пользуясь формулой Лагранжа и вторым из неравенств (16):
 ; (22)
; (22)
здесь  — число, заключенное между
— число, заключенное между  и
и  и, следовательно, удовлетворяющее неравенству
и, следовательно, удовлетворяющее неравенству  . Из (21) и (22) следует:
. Из (21) и (22) следует:
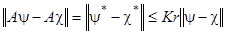 .
.
Таким образом, условие б) выполнено, если число 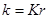 меньше единицы, т.е.
меньше единицы, т.е.
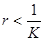 . (23)
. (23)
Итак, если число  удовлетворяет неравенствам (17), (20) и (23), то для семейства
удовлетворяет неравенствам (17), (20) и (23), то для семейства  выполнены условия а) и б). В дальнейшем будем считать число
выполнены условия а) и б). В дальнейшем будем считать число  выбранным таким образом, что неравенства (17), (20) и (23) для него выполнены.
выбранным таким образом, что неравенства (17), (20) и (23) для него выполнены.
Построим теперь последовательность
 (24)
(24)
функций, определенных на отрезке  , положив:
, положив:
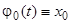 , (25)
, (25)
 (26)
(26)
Так как функция (25) принадлежит семейству  , то и все функции последовательности (24) принадлежат этому же семейству (см. условие а)). Далее мы имеем (см. (18)):
, то и все функции последовательности (24) принадлежат этому же семейству (см. условие а)). Далее мы имеем (см. (18)):  . В силу (19) получаем
. В силу (19) получаем 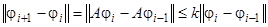 , откуда
, откуда  . Таким образом, в силу В), последовательность (24) равномерно сходится на отрезке
. Таким образом, в силу В), последовательность (24) равномерно сходится на отрезке  к некоторой непрерывной функции
к некоторой непрерывной функции 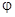 . Так как все функции последовательности (24) принадлежат семейству
. Так как все функции последовательности (24) принадлежат семейству  , то и функция
, то и функция 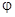 принадлежит ему (см. (18)). Покажем, что функция
принадлежит ему (см. (18)). Покажем, что функция 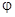 удовлетворяет уравнению (10). Для этого заметим, что последовательность
удовлетворяет уравнению (10). Для этого заметим, что последовательность  равномерно сходится к функции
равномерно сходится к функции  ; действительно, мы имеем
; действительно, мы имеем 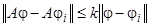 . Переходя в соотношении (26) к пределу при
. Переходя в соотношении (26) к пределу при 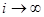 , получаем
, получаем  .
.
Итак, существование решения уравнения (1), удовлетворяющего начальному условию (6), доказано; при этом установлено, что решение  определено на интервале
определено на интервале  , где
, где  — произвольное число, удовлетворяющее неравенствам (17), (20) и (23).
— произвольное число, удовлетворяющее неравенствам (17), (20) и (23).
Перейдем теперь к доказательству единственности.Пусть  и
и 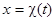 — два решения уравнения (1) с общими начальными значениями
— два решения уравнения (1) с общими начальными значениями  и
и  — интервал, являющийся пересечением интервалов существования решений
— интервал, являющийся пересечением интервалов существования решений  и
и  ; очевидно, что
; очевидно, что  . Покажем, что если решения
. Покажем, что если решения  и
и  совпадают в некоторой точке
совпадают в некоторой точке  интервала
интервала  , то они совпадают и на некотором интервале
, то они совпадают и на некотором интервале  , где
, где  — достаточно малое положительное число. Положим
— достаточно малое положительное число. Положим 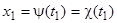 ; тогда величины
; тогда величины 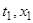 могут быть приняты за начальные значения обоих решений
могут быть приняты за начальные значения обоих решений  и
и 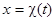 . В этом смысле точка
. В этом смысле точка 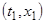 ничем не отличается от точки
ничем не отличается от точки  , и поэтому мы сохраним за точкой
, и поэтому мы сохраним за точкой 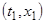 обозначение
обозначение  : это позволит нам сохранить и другие прежние обозначения. Переходя от дифференциального уравнения (1) к интегральному уравнению (7), мы получаем для обеих функций
: это позволит нам сохранить и другие прежние обозначения. Переходя от дифференциального уравнения (1) к интегральному уравнению (7), мы получаем для обеих функций  и
и  интегральные равенства, которые в операторной форме могут быть записаны в виде
интегральные равенства, которые в операторной форме могут быть записаны в виде
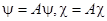 . (27)
. (27)
Выберем теперь, как и прежде, в открытом множестве  прямоугольник
прямоугольник  с центром в точке
с центром в точке  , а затем прямоугольник
, а затем прямоугольник  таким образом, чтобы число
таким образом, чтобы число  кроме неравенств (17), (20), (23) удовлетворяло еще и тому условию, что при
кроме неравенств (17), (20), (23) удовлетворяло еще и тому условию, что при  функции
функции  и
и  определены и удовлетворяют неравенствам
определены и удовлетворяют неравенствам 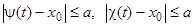 . Это возможно, так как функции
. Это возможно, так как функции  и
и  непрерывны. Тогда функции
непрерывны. Тогда функции  и
и  , рассматриваемые на отрезке
, рассматриваемые на отрезке  , входят в семейство
, входят в семейство  , и, следовательно, в силу неравенства (19) и соотношений (27) получаем
, и, следовательно, в силу неравенства (19) и соотношений (27) получаем 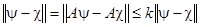 , а это возможно только тогда, когда
, а это возможно только тогда, когда  , т. е. когда функции
, т. е. когда функции  и
и  совпадают на отрезке
совпадают на отрезке  .
.
Докажем теперь, что функции  и
и  совпадают на всем интервале
совпадают на всем интервале  . Допустим противоположное, а именно, что существует точка
. Допустим противоположное, а именно, что существует точка  интервала
интервала  , для которой
, для которой 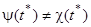 . Ясно, что
. Ясно, что 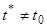 . Для определенности будем считать, что
. Для определенности будем считать, что  .
.
Обозначим через  множество всех тех точек
множество всех тех точек  отрезка
отрезка 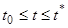 , для которых
, для которых  , и докажем, что множество
, и докажем, что множество  замкнуто. В самом деле, пусть
замкнуто. В самом деле, пусть 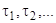 — последовательность точек множества
— последовательность точек множества  , сходящаяся к некоторой точке
, сходящаяся к некоторой точке  . Тогда
. Тогда 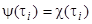 , и потому, в силу непрерывности функций
, и потому, в силу непрерывности функций  и
и  ,
,
 ,
,
т.е. точка  также принадлежит множеству
также принадлежит множеству  .
.
Обозначим через  точную верхнюю грань множества
точную верхнюю грань множества  . Так как
. Так как  замкнуто, то
замкнуто, то  принадлежит этому множеству, т.е.
принадлежит этому множеству, т.е. 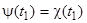 ; следовательно,
; следовательно,  . Но тогда, в силу ранее доказанного, функции
. Но тогда, в силу ранее доказанного, функции  и
и  должны совпадать на некотором интервале
должны совпадать на некотором интервале  , и точка
, и точка  не может быть точной верхней гранью множества
не может быть точной верхней гранью множества  . Таким образом, мы пришли к противоречию. Теорема доказана.
. Таким образом, мы пришли к противоречию. Теорема доказана.
Пример. Для весьма простого уравнения 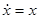 найдем решение методом последовательных приближений. Решение будем искать с начальными значениями
найдем решение методом последовательных приближений. Решение будем искать с начальными значениями 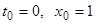 .
.
Соответствующее интегральное уравнение запишется в виде
 .
.
Будем строить теперь последовательность 
Мы имеем:

Пределом этой последовательности (равномерно сходящейся на любом отрезке числовой оси) является функция  .
.