Уравнения первого порядка, разрешенные относительно производной
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Лекция 2
Обыкновенное дифференциальное уравнение первого порядка первой степени можно, разрешив относительно производной, представить в виде  . Простейший пример такого уравнения
. Простейший пример такого уравнения  рассматривается в курсе интегрального исчисления. В этом простейшем случае решение
рассматривается в курсе интегрального исчисления. В этом простейшем случае решение  содержит произвольную постоянную, которая может быть определена, если известно значение
содержит произвольную постоянную, которая может быть определена, если известно значение  , тогда
, тогда  . В дальнейшем будет доказано, что при некоторых ограничениях, налагаемых на функцию
. В дальнейшем будет доказано, что при некоторых ограничениях, налагаемых на функцию  , уравнение
, уравнение  также имеет единственное решение, удовлетворяющее условию
также имеет единственное решение, удовлетворяющее условию  , а его общее решение, т.е. множество решений, содержащее все без исключения решения, зависит от одной произвольной постоянной.
, а его общее решение, т.е. множество решений, содержащее все без исключения решения, зависит от одной произвольной постоянной.
Дифференциальное уравнение  устанавливает зависимость между координатами точки и угловым коэффициентом касательной
устанавливает зависимость между координатами точки и угловым коэффициентом касательной  к графику решения в той же точке. Зная
к графику решения в той же точке. Зная 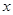 и
и  , можно вычислить
, можно вычислить  . Следовательно, дифференциальное уравнение рассматриваемого вида определяет поле направлений и задача интегрирования дифференциального уравнения заключается в том, чтобы найти кривые, называемые интегральными кривыми, направление касательных к которым в каждой точке совпадает с направлением поля.
. Следовательно, дифференциальное уравнение рассматриваемого вида определяет поле направлений и задача интегрирования дифференциального уравнения заключается в том, чтобы найти кривые, называемые интегральными кривыми, направление касательных к которым в каждой точке совпадает с направлением поля.
Пример 1.  . В каждой точке, отличной от точки (0,0), угловой коэффициент касательной к искомой интегральной кривой равен отношению
. В каждой точке, отличной от точки (0,0), угловой коэффициент касательной к искомой интегральной кривой равен отношению  , т.е. совпадает с угловым коэффициентом прямой, направленной из начала координат в ту же точку
, т.е. совпадает с угловым коэффициентом прямой, направленной из начала координат в ту же точку  . Очевидно, что интегральными кривыми в данном случае будут прямые
. Очевидно, что интегральными кривыми в данном случае будут прямые  , так как направления этих прямых всюду совпадают с направлением поля.
, так как направления этих прямых всюду совпадают с направлением поля.
Пример 2.  . Замечаем, что угловой коэффициент касательной к искомым интегральным кривым
. Замечаем, что угловой коэффициент касательной к искомым интегральным кривым  и угловой коэффициент касательной
и угловой коэффициент касательной  к интегральным кривым примера 1 в каждой точке удовлетворяют условию ортогональности:
к интегральным кривым примера 1 в каждой точке удовлетворяют условию ортогональности:  . Следовательно, поле направлений, определяемое рассматриваемым дифференциальным уравнением, ортогонально полю направлений, изображенному на рис. Очевидно, что интегральными кривыми уравнения
. Следовательно, поле направлений, определяемое рассматриваемым дифференциальным уравнением, ортогонально полю направлений, изображенному на рис. Очевидно, что интегральными кривыми уравнения  являются окружности с центром в начале координат
являются окружности с центром в начале координат  (точнее, полуокружности
(точнее, полуокружности  и
и  .
.
Пример 3.  . Для построения поля направлений найдем геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. Уравнение изоклин получим, считая
. Для построения поля направлений найдем геометрическое место точек, в которых касательные к искомым интегральным кривым сохраняют постоянное направление. Такие линии называются изоклинами. Уравнение изоклин получим, считая  , где
, где 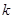 — постоянная;
— постоянная;  или
или  . Следовательно, в данном случае изоклинами являются окружности с центром в начале координат, причем угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Для построения поля направлений дадим постоянной
. Следовательно, в данном случае изоклинами являются окружности с центром в начале координат, причем угловой коэффициент касательной к искомым интегральным кривым равен радиусу этих окружностей. Для построения поля направлений дадим постоянной 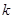 некоторые определенные значения. Теперь уже можно приближенно провести искомые интегральные кривые.
некоторые определенные значения. Теперь уже можно приближенно провести искомые интегральные кривые.
Пример 4.  . Изоклинами являются гиперболы
. Изоклинами являются гиперболы  или
или  , причем при
, причем при  гипербола распадается на пару прямых
гипербола распадается на пару прямых  и
и  . При
. При  получаем изоклину
получаем изоклину  ; эта гипербола разбивает плоскость на части, в каждой из которых
; эта гипербола разбивает плоскость на части, в каждой из которых  сохраняет постоянный знак. Интегральные кривые
сохраняет постоянный знак. Интегральные кривые  , пересекая гиперболу
, пересекая гиперболу  , переходят из области возрастания функции
, переходят из области возрастания функции  в области ее убывания или, наоборот, из области убывания в область возрастания, и следовательно, на ветвях этой гиперболы расположены точки максимума и минимума интегральных кривых.
в области ее убывания или, наоборот, из области убывания в область возрастания, и следовательно, на ветвях этой гиперболы расположены точки максимума и минимума интегральных кривых.
Определим теперь знаки второй производной в различных областях плоскости:  или
или  . Кривая
. Кривая  или
или
 (1)
(1)
разбивает плоскость на две части, в одной из которых  , и, следовательно, интегральные кривые выпуклы вверх, а в другой
, и, следовательно, интегральные кривые выпуклы вверх, а в другой  , и, следовательно, интегральные кривые вогнуты вверх (выпуклы вниз). При переходе через кривую (1) интегральные кривые переходят от выпуклости к вогнутости, и следовательно, на этой кривой расположены точки перегиба интегральных кривых.
, и, следовательно, интегральные кривые вогнуты вверх (выпуклы вниз). При переходе через кривую (1) интегральные кривые переходят от выпуклости к вогнутости, и следовательно, на этой кривой расположены точки перегиба интегральных кривых.
В результате проведенного исследования известны области возрастания и убывания интегральных кривых, известно расположение точек максимума и минимума, известны области выпуклости и вогнутости и расположение точек перегиба, известна изоклина  . Этих сведений вполне достаточно для того, чтобы сделать набросок расположения интегральных кривых, но можно было бы вычертить еще несколько изоклин, что позволило бы уточнить расположение интегральных кривых.
. Этих сведений вполне достаточно для того, чтобы сделать набросок расположения интегральных кривых, но можно было бы вычертить еще несколько изоклин, что позволило бы уточнить расположение интегральных кривых.
Во многих задачах, в частности почти во всех задачах геометрического характера, переменные 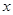 и
и  совершенно равноправны. Поэтому в таких задачах, если они сводятся к решению дифференциального уравнения
совершенно равноправны. Поэтому в таких задачах, если они сводятся к решению дифференциального уравнения
 (2)
(2)
естественно наряду с уравнением (2) рассматривать также уравнение
 . (3)
. (3)
Если оба эти уравнения имеют смысл, то они эквивалентны, так как если функция  является решением уравнения (2), то обратная функция
является решением уравнения (2), то обратная функция  является решением уравнения (3), и следовательно, уравнения (2) и (3) имеют общие интегральные кривые.
является решением уравнения (3), и следовательно, уравнения (2) и (3) имеют общие интегральные кривые.
Если же в некоторых точках одно из уравнений (2) или (3) теряет смысл, то в таких точках естественно его заменять другим из этих уравнений.
Например, уравнение  теряет смысл при
теряет смысл при  . Заменив его уравнением
. Заменив его уравнением  , правая часть которого уже не теряет смысла при
, правая часть которого уже не теряет смысла при  , находим в дополнение к ранее найденным решениям
, находим в дополнение к ранее найденным решениям  еще одну интегральную кривую
еще одну интегральную кривую  этого уравнения.
этого уравнения.
Уравнения с разделяющимися переменными
Дифференциальные уравнения вида
 (4)
(4)
называются уравнениями с разделенными переменными. Функции  и
и  будем считать непрерывными.
будем считать непрерывными.
Предположим, что  является решением этого уравнения, тогда при подстановке
является решением этого уравнения, тогда при подстановке  в уравнение (4) получим тождество, интегрируя которое, будем иметь
в уравнение (4) получим тождество, интегрируя которое, будем иметь
 , (5)
, (5)
где  — произвольная постоянная.
— произвольная постоянная.
Мы получили конечное уравнение (5), которому удовлетворяют все решения уравнения (4), причем каждое решение уравнения (5) является решением уравнения (4), так как если некоторая функция  при подстановке обращает уравнение (5) в тождество, то, дифференцируя это тождество, обнаружим, что
при подстановке обращает уравнение (5) в тождество, то, дифференцируя это тождество, обнаружим, что  удовлетворяет и уравнению (4).
удовлетворяет и уравнению (4).
Конечное уравнение  , которое определяет решение
, которое определяет решение  дифференциального уравнения как неявную функцию
дифференциального уравнения как неявную функцию 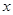 , называется интегралом рассматриваемого дифференциального уравнения.
, называется интегралом рассматриваемого дифференциального уравнения.
Если это конечное уравнение определяет все без исключения решения данного дифференциального уравнения, то оно называется общим интегралом рассматриваемого дифференциального уравнения. Следовательно, уравнение (5) является общим интегралов уравнения (4). Для того, чтобы уравнения (5) определяло  как неявную функцию
как неявную функцию 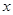 , достаточно потребовать, чтобы
, достаточно потребовать, чтобы  .
.
Вполне возможно, что в некоторых задачах неопределенные интегралы  и
и  нельзя будет выразить в элементарных функциях, тем не менее мы и в этом случае будем считать задачу интегрирования дифференциального уравнения (4) выполненной в том смысле, что мы свели ее к более простой и уже изученной в курсе матанализа задаче вычисления неопределенных интегралов — квадратур. Так как термин «интеграл» в теории дифференциальных уравнений часто применяется в смысле интеграла дифференциального уравнения, то во избежание недоразумений для интегралов функций
нельзя будет выразить в элементарных функциях, тем не менее мы и в этом случае будем считать задачу интегрирования дифференциального уравнения (4) выполненной в том смысле, что мы свели ее к более простой и уже изученной в курсе матанализа задаче вычисления неопределенных интегралов — квадратур. Так как термин «интеграл» в теории дифференциальных уравнений часто применяется в смысле интеграла дифференциального уравнения, то во избежание недоразумений для интегралов функций  обычно применяется термин «квадратура».
обычно применяется термин «квадратура».
Если надо выделить частное решение, удовлетворяющее условию  , то оно, очевидно, определится из уравнения
, то оно, очевидно, определится из уравнения  . Определим константу. Удовлетворяя начальному условию, т.е. подставляя
. Определим константу. Удовлетворяя начальному условию, т.е. подставляя  , получим
, получим  , откуда искомое частное решение в неявной форме определяется интегралом
, откуда искомое частное решение в неявной форме определяется интегралом  .
.
Пример 1.  . Переменные разделены, так как коэффициент при
. Переменные разделены, так как коэффициент при  является функцией только
является функцией только 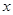 , а коэффициент при
, а коэффициент при  является функцией только
является функцией только  . Интегрируя, получим
. Интегрируя, получим  или
или  — семейство окружностей с центром в начале координат.
— семейство окружностей с центром в начале координат.
Пример 2.  . Интегрируя, получаем
. Интегрируя, получаем  . Интегралы
. Интегралы  и
и  не берутся в элементарных функциях, тем не менее исходное уравнение считается проинтегрированным, так как задача доведена до квадратур.
не берутся в элементарных функциях, тем не менее исходное уравнение считается проинтегрированным, так как задача доведена до квадратур.
Уравнения вида  , в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от
, в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от 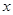 и только от
и только от  , называются дифференциальными уравнениями с разделяющимися переменными, так как путем деления на
, называются дифференциальными уравнениями с разделяющимися переменными, так как путем деления на  они приводятся к уравнению с разделенными переменными:
они приводятся к уравнению с разделенными переменными:  . Заметим, что деление на
. Заметим, что деление на  может привести к потере частных решений, обращающих в нуль произведение
может привести к потере частных решений, обращающих в нуль произведение  , а если функции
, а если функции  и
и  могут быть разрывными, то возможно появление лишних решений, обращающих в нуль множитель
могут быть разрывными, то возможно появление лишних решений, обращающих в нуль множитель  .
.
Пример 3.  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:  . Потенцируя, получим
. Потенцируя, получим  . Если речь идет только о гладких решениях, то уравнение
. Если речь идет только о гладких решениях, то уравнение  , где
, где  , эквивалентно уравнению
, эквивалентно уравнению  или
или  , где
, где  может принимать как положительные, так и отрицательные значения, но не равняться нулю. Если же принять во внимание, что при делении на
может принимать как положительные, так и отрицательные значения, но не равняться нулю. Если же принять во внимание, что при делении на  мы потеряли решение
мы потеряли решение  , то можно считать, что в решении
, то можно считать, что в решении  постоянная
постоянная  может и равняться нулю. При этом мы получаем потерянное ранее решение
может и равняться нулю. При этом мы получаем потерянное ранее решение  .
.
Если в этом примере считать переменные 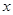 и
и  равноправными, то уравнение
равноправными, то уравнение  , теряющее смысл при
, теряющее смысл при  , надо дополнить уравнением
, надо дополнить уравнением  , как мы делали ранее. Такое уравнение, очевидно, имеет еще решение
, как мы делали ранее. Такое уравнение, очевидно, имеет еще решение  , не содержащееся в найденном выше решении
, не содержащееся в найденном выше решении  .
.
Пример 4.  . Разделяем переменные и интегрируем:
. Разделяем переменные и интегрируем:

Пример 5.  . Найти решение
. Найти решение  , удовлетворяющее условию
, удовлетворяющее условию  .
.
Разделяем переменные и интегрируем:
 .
.
Пример 6. Пусть  — потенциал скоростей плоскопараллельного течения жидкости. Найти уравнение линий тока.
— потенциал скоростей плоскопараллельного течения жидкости. Найти уравнение линий тока.
Линии тока являются ортогональными траекториями семейства эквипотенциальных линий  . Находим угловой коэффициент касательной к эквипотенциальным линиям:
. Находим угловой коэффициент касательной к эквипотенциальным линиям:  . Следовательно, дифференциальное уравнение линий тока имеет вид
. Следовательно, дифференциальное уравнение линий тока имеет вид  , или
, или  ; интегрируя, получаем
; интегрируя, получаем  — семейство гипербол.
— семейство гипербол.
Пример 7. Полый однородный металлический шар, имеющий внутренний радиус  , а внешний
, а внешний  , находится в стационарном тепловом состоянии, причем температура на его внутренней поверхности равна
, находится в стационарном тепловом состоянии, причем температура на его внутренней поверхности равна  , а на наружной
, а на наружной  . Найти температуру
. Найти температуру 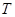 на расстоянии
на расстоянии  от центра шара,
от центра шара,  .
.
Из соображений симметрии следует, что 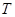 является функцией только
является функцией только  .
.
Так как между двумя концентрическими сферами с центрами в центре шара (их радиусы могут изменяться от  до
до  ) количество тепла остается неизменным, то через каждую сферу протекает одно и то же количество тепла
) количество тепла остается неизменным, то через каждую сферу протекает одно и то же количество тепла  . Следовательно, дифференциальное уравнение, описывающее рассматриваемый процесс, имеет вид
. Следовательно, дифференциальное уравнение, описывающее рассматриваемый процесс, имеет вид  , где
, где 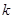 — коэффициент теплопроводности.
— коэффициент теплопроводности.
Разделяя переменные и интегрируя, получим искомую зависимость  :
:

Для определения  используем условие: при
используем условие: при  :
:
 .
.
Рассмотрим теперь несколько другую запись. Дифференциальное уравнение  называется уравнением с разделяющимися переменными, если его правая часть представима в виде
называется уравнением с разделяющимися переменными, если его правая часть представима в виде  . В случае, когда
. В случае, когда  , общее решение уравнения с разделяющимися переменными задается соотношением
, общее решение уравнения с разделяющимися переменными задается соотношением  .
.
Пример 8. Пусть  . Это уравнение с разделяющимися переменными, так как
. Это уравнение с разделяющимися переменными, так как  , а
, а  .
.
Пусть  , тогда
, тогда  , или
, или  . Поскольку
. Поскольку  , то общее решение исходного уравнения
, то общее решение исходного уравнения  , где
, где  — произвольная постоянная.
— произвольная постоянная.
Уравнения, приводящиеся к уравнениям с разделяющимися переменными.
Многие дифференциальные уравнения путем замены переменных могут быть приведены к уравнениям с разделяющимися переменными. К числу таких уравнений относятся, например, уравнения вида
 ,
,
где  — постоянные величины, которые заменой переменных
— постоянные величины, которые заменой переменных  преобразуются в уравнения с разделяющимися переменными. Действительно, переходя к новым переменным
преобразуются в уравнения с разделяющимися переменными. Действительно, переходя к новым переменным  , будем иметь
, будем иметь
 ,
,
или  , и переменные разделились. Интегрируя, получим
, и переменные разделились. Интегрируя, получим
 .
.
Пример 1.  .
.
Полагая  , будем иметь
, будем иметь
 .
.
Разделяя переменные и интегрируя, получим

Пример 2.  .
.
Полагая  , получим
, получим

К уравнениям с разделяющимися переменными приводятся и так называемые однородные дифференциальные уравнения первого порядка, имеющие вид  .
.
Действительно, после подстановки  или
или  получим
получим

Другая запись. Дифференциальное уравнение  называется однородным, если
называется однородным, если  — однородная функция нулевой степени.
— однородная функция нулевой степени.
Функция  называется однородной степени
называется однородной степени 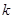 , если для любого
, если для любого  выполняется равенство
выполняется равенство
 (6)
(6)
Например, функции  являются однородными степени соответственно 0, 1, 2,
являются однородными степени соответственно 0, 1, 2,  .
.
Замена
 (7)
(7)
приводит при  однородное уравнение к уравнению с разделяющимися переменными. Действительно, так как
однородное уравнение к уравнению с разделяющимися переменными. Действительно, так как  — однородная функция нулевой степени, то из (6) получаем равенство
— однородная функция нулевой степени, то из (6) получаем равенство
 . (8)
. (8)
Из (7) имеем
 . (9)
. (9)
Подставив (8) и (9) в исходное уравнение  , получаем уравнение с разделяющимися переменными
, получаем уравнение с разделяющимися переменными  . В случае
. В случае  аналогичный результат достигается заменой
аналогичный результат достигается заменой  .
.
Заметим, что правая часть однородного уравнения является однородной функцией переменных  нулевой степени однородности, поэтому уравнение вида
нулевой степени однородности, поэтому уравнение вида  (либо, в другой записи,
(либо, в другой записи,  ) будет однородным, если
) будет однородным, если  и
и  являются однородными функциями
являются однородными функциями 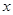 и
и  одинаковой степени однородности, так как в этом случае
одинаковой степени однородности, так как в этом случае
 .
.
Пример 3.  .
.
Полагая  и подставляя в исходное уравнение получим
и подставляя в исходное уравнение получим

Пример 4.  .
.
Полагая  , получим
, получим


Пример 5.  .
.
Положив  , получим
, получим  . Далее
. Далее  .
.
Дифференциальное уравнение вида
 (10)
(10)
называется обобщенным однородным уравнением. Оно приводится к однородному линейной заменой
 , (11)
, (11)
где  — координаты точки пересечения прямых
— координаты точки пересечения прямых

Фактически, мы переносим начало координат в точку пересечения прямых.
Действительно, в этом случае справедливы равенства:

Поэтому, в силу (11), правая часть уравнения (10) принимает вид
 .
.
Кроме того, из (11) получаем  . Таким образом, уравнение (10) переходит в уравнение
. Таким образом, уравнение (10) переходит в уравнение  , правая часть которого есть однородная функция нулевой степени, в силу чего последнее уравнение является однородным.
, правая часть которого есть однородная функция нулевой степени, в силу чего последнее уравнение является однородным.
Если же наши прямые не пересекаются, то в этом случае  и, следовательно,
и, следовательно,  . Тогда (10) переходит в уравнение
. Тогда (10) переходит в уравнение
 ,
,
которое приводится к уравнению с разделяющимися переменными путем замены  .
.
Пример 6.  .
.
Перепишем уравнение в форме
 . (12)
. (12)
Это уравнение является обобщенным однородным. Чтобы привести его к однородному, найдем точку пересечения прямых
 (13)
(13)
Из (13) получаем  . В уравнении (12) производим замену
. В уравнении (12) производим замену

и получаем однородное уравнение  . В полученном уравнении положим
. В полученном уравнении положим  . Тогда имеем:
. Тогда имеем:
 . (14)
. (14)
Функция  является решением полученного уравнения. Остальные его решения найдем, разделяя переменные:
является решением полученного уравнения. Остальные его решения найдем, разделяя переменные:
 , или
, или
 . (15)
. (15)
Решения  получаем из формулы (15) при
получаем из формулы (15) при  .
.
Переходя к переменным  , получим
, получим  .
.
Пример 7.  .
.
Решая систему уравнений  , получим
, получим  . Полагая
. Полагая  , будем иметь
, будем иметь
 .
.
Замена переменных  или
или  приводит к уравнению с разделяющимися переменными
приводит к уравнению с разделяющимися переменными
 ,
, 

Дифференциальное уравнение  называется квазиоднородным, если функция
называется квазиоднородным, если функция  является квазиоднородной степени
является квазиоднородной степени  , т.е. если при
, т.е. если при  выполняется соотношение
выполняется соотношение
 . (16)
. (16)
Замена
 (17)
(17)
приводит квазиоднородное уравнение к однородному. Действительно, в силу (16), положив  , получаем
, получаем
 . (18)
. (18)
Подставляя  в исходное уравнение, получаем
в исходное уравнение, получаем
 , откуда, в силу (18),
, откуда, в силу (18),  .
.
Последнее уравнение является однородным.
Пример 8.  .
.
Чтобы данное уравнение было квазиоднородным, необходимо, в силу (16), чтобы
 ,
,
или  ,
,
т.е. чтобы система уравнений  была совместной. Эта система эквивалентна одному уравнению
была совместной. Эта система эквивалентна одному уравнению  , имеющему бесчисленное множество решений. Таким образом, исходное уравнение является квазиоднородным. Чтобы привести его к однородному уравнению, производим замену
, имеющему бесчисленное множество решений. Таким образом, исходное уравнение является квазиоднородным. Чтобы привести его к однородному уравнению, производим замену  , в результате которой получаем
, в результате которой получаем  . Последнее уравнение является однородным.
. Последнее уравнение является однородным.