Лекция 7 (2ч.) Показатели вариации.
.
Средняя гармоническая (простая и взвешенная) применяется, когда характер исходных статистических данных таков, что расчет средней арифметической теряет смысл. Если известны численные значения числителя логической формулы, а значениязнаменателя не известны, но могут быть найдены как частное от деления одного показателя на другой, то средняя величина вычисляется по формуле средней гармонической взвешенной:
.
Средняя гармоническая(простая) применяется когда веса всех вариантов (fi) равны:
,
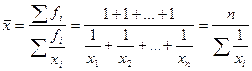где хi - отдельные варианты, n - число вариантов осредняемого признака.
Средняя квадратическая применяется при расчете с величинами квадратных функций, используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения.
Средняя кубическая применяется при расчете с величинами кубических функций.
Структурные средние характеризуют состав статистической совокупности по одному из варьирующих признаков. К этим средним относятся мода и медиана.
Мода - это значение варьирующего признака, которое в данном ряду распределения имеет наибольшую частоту. В дискретных рядах распределений мода определяется визуально. Сначала определяется наибольшая частота, а по ней модальное значение признака. В интервальных рядах для вычисления моды используется следующая формула:
- нижняя граница модального интервала (интервал с наибольшей частотой),
- величина модального интервала (шаг),
- частота модального интервала,
- частота интервала предшествующего модальному,
- частота интервала следующего за модальным.
Пример. Найдем модальный размер обуви по магазину со следующими данными:
Таблица.
| Размер обуви | 31 - 33 | 33 - 35 | 35 - 37 | 37 - 40 | 40 - 43 |
| Число купленных пар |
- нижняя граница модального интервала, так как 20 пар обуви наибольшая частота,
- величина модального интервала,
- частота модального интервала,
- частота интервала предшествующего модальному,
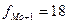- частота интервала следующего за модальным.
Таким образом, 
. Следовательно, самый востребованный размер обуви по данному магазину - 36,5
Графический способ нахождения моды.
 |
Рисунок 7.1.
Пост
Строим столбиковую диаграмму – гистограмму распределения. В
гистограмме основания столбиков расположены на оси абсцисс – это
интервалы варьирующего признака. А высота столбиков – это частоты соответствующие масштабу по оси ординат. Выстроив столбики, визуально определяем самый высокий. Этот столбик соответствует модальному интервалу изучаемого признака. Из левого угла этого столбика проводим прямую линию до левого верхнего угла столбика следующего за модальным. Из правого угла модального столбика проводим прямую линию до правого угла столбика стоящего перед модальным. Из точки пересечения опустим прямую линию до пересечения с осью абсцисс. Мода находится в точке пересечения с осью ОХ.
Медианой называется такое значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот. Медиана рассчитывается различными способами в дискретных и интервальных рядах.
Если ряд распределения дискретный и состоит из четного числа членов, то медиана определяется как средняя величина из двух серединных значений ранжированного ряда признаков.
Пример. Имеются данные о дневной выручке магазина, при шестидневной рабочей неделе (тыс. руб.):
| понедельник | вторник | среда | четверг | пятница | суббота |
Для начала необходимо построить ранжированный вариационный ряд. То есть расположить выручку магазина в порядке возрастания:
100; 150; 200; 300; 500; 700.
Медиана находится между третьим (200) и четвертым (300) значением выручки – (200+300)/2=250 тыс.руб.
Если в дискретном ряду распределения нечетное число уровней, то медианой будет серединное значение ранжированного ряда признаков.
Пример. Имеются данные о дневной выручке магазина, при семидневной рабочей неделе (тыс. руб.):
| понедельник | вторник | среда | четверг | пятница | суббота | воскресенье |
Снова построим ранжированный вариационный ряд: 100; 150; 200; 300; 400; 500; 700.
Медиана проходит по четвертому значению т.е. медианная (серединная) выручка составляет 300 тыс.руб.
В интервальных рядах медиана определяется по формуле:
- нижняя граница медианного интервала (интервала для которого накопленная частота впервые превысит полусумму частот)
- величина медианного интервала (шаг)
- сумма частот ряда
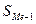- сумма накопленных частот предшествующих медианному интервалу
- частота медианного интервала
Пример. Найдем медианный размер обуви по нижеприведенным данным.
Таблица.
| Размер обуви | Число купленных пар | Сумма накопленных частот |
| 31-33 | ||
| 33-35 | ||
| 35-37 | ||
| 37-40 | ||
| 40-43 |
Чтобы найти медианный интервал рассчитаем полусумму накопленных (кумулятивных) частот: 
. В интервале 37-40 накопленная частота превысила, найденное значение полусуммы частот (50 > 34,5). Следовательно, интервал 37-40 – медианный. Тогда,
- нижняя граница медианного интервала,
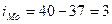- величина медианного интервала,
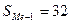- накопленная частота в интервале перед медианным,
- частота в медианном интервале.
Рассчитаем медиану: 
. Таким образом, половина всей проданной обуви больше размера 37,5 (37,4). Соответственно, другая половина проданной обуви меньше медианного размера.
Графический метод нахождения медианы.
Для этого строим график по накопленным частотам – кумуляту распределения. На оси абсцисс откладываются значения дискретного признака (или границы интервала), а на оси ординат – нарастающие итоги частот или частостей, соответствующие этим значениям признака (или верхним границам интервалов). Затем соединяем, отмеченные точки ломаной линией. Из точки на оси ординат, соответствующей полусумме накопленных частот (34,5), проводим прямую до пересечения с кумулятой (точка Z). Из точки пересечения Z опускаем перпендикуляр на прямую ОХ. Координата, найденной точки пересечения с осью ОХ и является медианой. В нашем примере, координата оказывается равной 37,5. Графический и расчетный методы, приводят к одинаковым результатам.
К структурным средним относятcя также квартиль, дециль, перцентиль. Квартиль(Q) –значение признака, которое делит ранжированный (упорядоченный) ряд на четыре равные части.
 |
Рисунок 5–Деление ряда на квартили
При этом получается три величины – первая квартиль (
), вторая квартиль (
), третья квартиль (
). Расчет квартилей показывает, что четверть единиц совокупности не превышает значения первой квартили, половина единиц совокупности не превышает значения второй квартили, и три четверти единиц совокупности не превышает значения третьей квартили. Следует заметить, что вторая квартиль является медианой.
Дециль делит упорядоченный ранжированный ряд на 10 частей. Перцентиль на 100 равных частей.
Термин "вариация" произошел от латинского variatio – “изменение, колеблемость, различие”. Вариацией называется различие значений признака у отдельных единиц совокупности. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов.
Вариация возникает в силу того, что отдельные значения признака формируются по влияние большого числа взаимосвязанных факторов. Эти факторы часто действуют в противоположных направлениях, и их совместное действие формирует значение признаков у конкретной единицы совокупности. Необходимость изучения вариаций связана с тем, что средняя величина, обобщающая данные статистического наблюдения, не показывает, как колеблется вокруг нее индивидуальное значение признака. Вариации присущи явлениям природы и общества. При этом изменения в общественных явлениях происходят быстрее, чем аналогичные изменения в природе. Объективно существуют также вариации в пространстве и во времени.
Вариация в пространстве показывает различие статистических показателей относящихся к различным административно-территориальным единицам.
Вариация во времени показывает различие показателей в зависимости от периода или момента времени, к которым они относятся.
Различают вариацию признака: случайную и систематическую.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а следовательно, насколько характерной является исчисленная средняя величина. Степень близости значений отдельных единиц 
к средней измеряется рядом абсолютных, средних и относительных показателей. Колеблемость отдельных значений характеризуют показатели вариации.
Абсолютные и средние показатели вариации и способы их расчета. Для характеристики совокупностей и вычисленных величин важно знать, какая вариация изучаемого признака скрывается за средней величиной.
Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.
Размах вариации - это разность между наибольшим (
) и наименьшим (
) значениями вариантов. 
Пример. Имеются данные о группировке предприятий по объему товарооборота:
Таблица
Группы предприятий по объему товарооборота, млн.руб. 
| Число предприятий 
|
| 90 — 100 | |
| 100 — 110 | |
| 110 — 120 | |
| 120 — 130 | |
| ИТОГО |
Определим показатель размаха вариации:
R = 130 - 90 = 40 млн. руб.
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
Чтобы дать обобщающую характеристику распределения отклонений, вычисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
.
Порядок расчета среднего линейного отклонения следующий:
1) по значениям признака вычисляется средняя арифметическая:
;
2) определяются отклонения каждой варианты 
от средней 
;
3) рассчитывается сумма абсолютных величин отклонений: 
;
4) сумма абсолютных величин отклонений делится на число значений:
.
Пример:
Таблица
| Табельный номер рабочего |
|
| 
|
| - 8 | |||
| - 7 | |||
| Итого |
.
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение вычисляется по формуле средней арифметической взвешенной:
Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная:
;
2) определяются абсолютные отклонения вариант от средней ;
3) полученные отклонения умножаются на частоты 
;
4) находится сумма взвешенных отклонений без учета знака:
;
5) сумма взвешенных отклонений делится на сумму частот:
.
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.
Основными обобщающими показателями вариации в статистике являются дисперсия и среднее квадратическое отклонение.
Дисперсия - это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается 
. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
— дисперсия невзвешенная (простая);
— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
— среднее квадратическое отклонение невзвешенное;
— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерой надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенной:
1) определяют среднюю арифметическую взвешенную
;
2) определяются отклонения вариант от средней 
;
3) возводят в квадрат отклонение каждой варианты от средней 
;
4) умножают квадраты отклонений на веса (частоты) 
;
5) суммируют полученные произведения
;
6) Полученную сумму делят на сумму весов
.
Пример:
Таблица
| Производительность, шт. (варианта)
| Кол-во раб.,
| 
| 
| 
| 
|
| -2 | |||||
| -1 | |||||
| ИТОГО |
Вычислим среднюю арифметическую взвешенную:
шт.
Значения отклонений от средней и их квадратов представлены в таблице. Определим дисперсию:
.
Среднее квадратическое отклонение будет равно:
шт.
Пример. Рассчитаем дисперсию в дискретном ряду распределения, используя вместо частот частости. Исходные данные представлены в виде дискретного ряда:
|
| |||||
|
Первая операция для нахождения дисперсии – расчет частостей на основе частот. Частость это относительная величина, которая рассчитывается следующим образом: 
.
Далее для нахождения дисперсии, как промежуточную величину, необходимо определить среднюю арифметическую:
, 
.
Поскольку ряд дискретный - интегральную форму нахождения дисперсии применять не следует, достаточно рассчитать центральный момент второго порядк: 
, 
.
Все шаги расчета целесообразно свести в таблицу:
|
| |||||
|
| |||||
| 0,1452 | 0,2581 | 0,3064 | 0,1774 | 0,1129 |
| 3,9204 | 9,2916 | 9,8048 | 7,6282 | 4,2902 |
| -7,9352 | 1,0648 | -2,9352 | 8,0648 | 3,0648 |
| 62,9674 | 1,1338 | 8,6154 | 65,0410 | 9,3930 |
| 9,1429 | 0,2926 | 2,6398 | 11,5383 | 1,0605 |
Если исходные данные представлены в виде интервального ряда распределения, то сначала надо определить дискретное значение признака, а далее применить те же методы, что изложены выше.
Пример. Покажем расчет дисперсии для интервального ряда на примере данных о распределении студентов по группам пропусков занятий за семестр (фрагмент таблицы):
Таблица
| Кол-во пропусков (х) | Кол-во студентов (n) |
|
| 
|
|
|
| 14 - 16 | -3,4 | 11,56 | ||||
| 16 - 18 | -1,4 | 1,96 | ||||
| 18 - 20 | 0,6 | 0,36 | ||||
| 20 - 22 | 2,6 | 6,76 | ||||
| ИТОГО |
Средняя арифметическая равна:
ц с 1га.
Вычислим дисперсию:
Дисперсия по индивидуальным данным и в рядах распределения может быть рассчитана по следующей формуле: 
.
Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Свойства дисперсии:
Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака в какое-то 
число раз, соответственно уменьшает или увеличивает дисперсию в 
раз, а среднее квадратическое отклонение - в раз.
Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной: 
. Если А равна нулю, то приходим к следующему равенству: 
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую ;
2) возводят в квадрат среднюю арифметическую
;
3) возводят в квадрат каждую варианту ряда 
;
4) находим сумму квадратов вариант 
;
5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат 
;
6) определяют разность между средним квадратом признака и квадратом средней 
.
Пример. Имеются следующие данные о написании пяти студентами контрольной работы, оцененной по 15-ти бальной шкале:
Таблица 5
| № студента | Результат (балл) | 
|
| ИТОГО |
Произведем следующие расчеты:
- средний балл в группе студентов,
.
Рассчитаем дисперсию в дискретном ряду распределения, используя данные следующей таблицы:
| Результат (баллов) (х) | Число студентов, n | 
| 
|
|
| ИТОГО |
Рассмотрим расчет дисперсии в интервальном ряду распределения.
Порядок расчета дисперсии взвешенной (по формуле ):
1) определяют среднюю арифметическую 
;
2) возводят в квадрат полученную среднюю 
;
3) возводят в квадрат каждую варианту ряда 
;
4) умножают квадраты вариант на частоты 
;
5) суммируют полученные произведения 
;
6) делят полученную сумму на сумму весов и получают средний квадрат признака 
;
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .
Пример. Имеются данные о распределении студентов по числу пропусков:
Таблица
| Кол-во пропусков занятий | Кол-во студентов |
|
|
|
|
| 14 - 16 | |||||
| 16 - 18 | |||||
| 18 - 20 | |||||
| 20 - 22 | |||||
| ИТОГО |
В подобных примерах прежде всего определяется дискретное значение признака в каждом интервале, а затем применяется метод расчета, указанный выше:
Средняя величина отражает тенденцию развития, т.е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.
Показатели относительного рассеивания.
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней:
.
2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений в средней величине:
.
3. Коэффициент вариации.
.
Учитывая, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. При этом исходят из того, что если V больше 40 %, то это говорит о большой колеблемости признака в изучаемой совокупности.