IV) Проявление «золотого сечения» в Солнечной системе.

Понятие «золотого сечения» известно ещё со времен Евклида. Его сущность состоит в том, что отрезок прямой делится на две части в среднем и крайне отношении, т.е. целое относится к большей части отрезка так же, как большая его часть относится к меньшей части. Решение этой задачи сводится к решению квадратного уравнения следующего вида:

Х2 – Х – 1 = 0; (9) Два корня этого уравнения имеют вид:

Х1 = 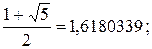(10) Х2 = (11)

Корень Х1 назван числом Фидия (Ф) в честь великого древнегреческого скульптора, жившего в 5 веке до нашей эры, скульптуры которого отличались высочайшей гармонией. Отношение отрезков, равное числу Фидия, или «золотому числу», и названо «золотым сечением».

Итак Х1 = Ф, а Х2 = - Ф-1. «Золотое сечение» находит свое проявление в пропорциях живых организмов, особенно, цветов растений и наиболее изящных животных. Это сечение пронизывает пропорции скульптур и архитектурных сооружений великих мастеров античности, а также музыкальные произведения замечательных композиторов. Числовой ряд Фибоначчи:

(0,1,1,2,3,5,8,13,21,34,55,144,233,377,610,987…) Fk+1= Fk + Fk-1; (12) и числовой ряд Люка:

(2,1,3,4,7,11,18,29,47,76,123,199,322,521,843…) Lk+1= Lk + Lk-1; (13),каждый последующий член которых равен сумме двух предыдущих членов ряда связаны с «золотым числом» следующим соотношением: (14)

при этом как числа Фибоначчи, так и числа Люка могут быть выражены через степени числа

Ф по следующим формулам:

Fk = ; (15) Lk = ; (16)

Поэтому, если при описании каких-либо параметров тел Солнечной системы мы сталкиваемся с числами Фибоначчи или Люка, это есть верный признак связи данного параметра с «золотым сечением». Как показали исследования, «золотое сечение», или «золотая пропорция», проявляют себя в следующих параметрах:

1)Обратных эксцентриситетах(смотри Таблицу 10)

Таблица 10

Тело е 1/ e N d%
П 0,24864 4,021879 0,55
Ме 0,20562 4,863340 2,81
Ма 0,09336 10,711225 2,70
Ц 0,07600 13,157894 1,21
С 0,05572 17,946877 0,30
Ю 0,04842 20,652622 1,68
У 0,04718 21,195421 0,93
З 0,01673 59,772863 8,68
Н 0,00857 116,68611 5,41
В 0,00680 147,05882 2,12
    среднее   2,64

В Таблице использованы следующие обозначения: e- эксцентриситеты орбит, n-числа Фибоначчи и Люка, d% - отклонение обратных значений эксцентриситетов от этих чисел в процентах.

2)Массах планет(смотри Таблицу 11).

Таблица 11

Тело m k Фk n n×Фk d%
Ю 317,37 321,9936 321,9936 1,45
С 95,08 46,97839 93,95678 1,20
Н 17,23 17,94417 17,94417 4,14
У 14,61 29,03426 0,5 14,51713 0,64
З 1,0000 1,000000 1,000000 0,00
В 0,8136 1,618034 0,5 0,809017 0,57
Ма 0,1069 -6 0,055728 0,111456 4,26
Ме 0,0543 -6 0,055728 0,055728 2,63
          среднее 1,86

В таблице приняты следующие обозначения: m – масса планет, выраженная в земных массах, k и n – целые и полуцелые числа, Ф – число Фидия, d% -отклонение расчетных значений масс от опытных в процентах.

3) Периодах обращений планет.

Мгновенные периоды обращения планет могут быть вычислены по следующим формулам:

Тp = Т0×(1-е)2; (17) Тa = Т0×(1+е)2; (18)

Где Тp иТa - мгновенные периоды обращений планет в перигелии и афелии, а Т0 – средний период соответственно, е – эксцентриситет орбиты, Np, Na и N0 – ближайшие к этим периодам значения чисел Люка и Фибоначчи. Для Нептуна в качестве Np взята половина числа Люка (322).

Таблица 12

Тело е Tp(сут.) Np d% T0(сут.) N0 d% Ta(сут.) Na d%
Ме 0,20562 55,512 0,93 87,970 1,17 127,866 3,96
В 0,00680 221,655     224,701     227,767 2,30
З 0,01673 353,123     365,242     377,565 0,15
Ма 0,09336 564,711     686,980     821,264 2,64
                среднее   1,86

Таблица 13

Тело е Tp(лет) Np d% Т0(лет) N0 d% Ta(лет) Na d%
Ц 0,076 3,932 1,74 4,605     5,332    
Ю 0,04842 10,741 2,41 11,862     13,039 0,30
С 0,05572 26,266     29,458 1,58 32,832 3,56
У 0,04718 76,274 0,36 84,015     92,130 3,52
Н* 0,00857 161,975 0,61 164,788     167,624    
П 0,24864 139,835 2,98 247,697     386,184 2,47
                среднее   1,95

Из анализа таблиц следует, что средние отклонения периодов от чисел Люка и Фибоначчи имеют величину меньше 2%.

4) Кольцевые частоты, отнесенные к аналогичной частоте Нептуна, соответствует числам Люка и Фибоначчи.Смотри Таблицу 14, где n - кольцевая частота планеты, nн –кольцевая частота Нептуна, N- ближайшее к отношению частот число Люка или Фибоначчи. Из анализа

Таблица 14

Тело n (год)-1 n / nн N (n/nн):N d%
Н 0,000156 1,0000 1,00000 1,62
У 0,001690 10,8346 0,98496 3,17
П 0,003305 21,1871 1,00890 0,72
С 0,057000 36,5384 1,07465 5,75
Ю 0,012286 78,7564 1,03626 1,97
В 0,033516 312,564 1,06816 5,11
З 0,050200 321,794 0,00036 1,68
Ц 0,049938 320,051 0,99394 2,23
Ма 0,150818 966,782 0,97951 3,69
        1,01619 2,88

таблицы следует, что данная закономерность соблюдается со средней ошибкой менее 3%. Числа Люка и Фибоначчи проявляют себя и также в объемах, орбитальных моментах и других параметрах планет.

Литература

1. Бутусов К.П. Свойства симметрии и дискретности гравитационных систем Солнца и планет. Совещание «Симметрия в природе». Л-д. 1971.

2. Бутусов К.П. Свойства симметрии Солнечной системы. Сб. «Некоторые проблемы исследования Вселенной»,вып.1. Изд. ВАГО СССР. Л-д. 1973.

3. Бутусов К.П. Дискретные свойства Солнечной системы. Сб. «Некоторые проблемы исследования Вселенной», вып.1. Изд. ВАГО СССР. Л-д. 1973.

4. Бутусов К.П. «Золотое сечение» в Солнечной системе. Сб. «Некоторые проблемы исследования Вселенной», вып.7. Изд. ВАГО СССР. Л-д. 1978.

5. Бутусов К.П. Качественный анализ решений дифференциальных уравнений волновых процессов.Автореферат диссертации. Изд. ЛГУ.1987.

6. Бутусов К.П. Новая инварианта, единая для электромагнитных и гравитационных систем. ЖРФМ № 1-6, 1995.