Лекция 6. Системы счисления
Системы счисления - это системы, созданные человеком (искусственные системы) . Существуют естественные системы, созданные природой. К естественным системам относятся галактики, солнечная система.
Разновидности искусственных систем.
- Материальные: автомобили, самолёты, дома, города.
- Общественные: различные объединения людей.
- Информационные: национальные языки, компьютерная сеть Internet, системы счисления и т.д.
Каждая искусственная система создаётся с определённой целью. Целью создания системы счисления является выработка наиболее простого способа записи чисел (к примеру, если бы у нас на каждой руке было четыре пальца, то, вероятнее всего, наша система счисления была бы не десятичной, а восьмеричной). Способов записи чисел цифровыми знаками существует бесчисленное множество.
Любая предназначенная для практического применения СС должна обеспечивать:
- возможность представления любого числа в рассматриваемом диапазоне величин;
- единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
- простоту оперирования числами;
Для записи чисел применяются и применялись издавна придуманные людьми специальные значки, называемые цифрами. Например, известны римские и арабские цифры.
С помощью римских цифр. Такая форма записи чисел применяется только в специфических случаях, например, в часах, датах, при нумерации. С помощью римских цифр неудобно записывать большие числа и при выполнении вычислений возникают серьезные проблемы.
С помощью арабских цифр (0, ……….9). Такая форма записи сложилась в Индии, а в Европе она стала известной благодаря арабским математикам. Особый вклад в популяризацию современной формы записи чисел сделал арабский математик аль-Хорезми, который сформулировал правила четырех арифметических действий (сложение, вычитание, умножение, деление) над многозначными числами.
Существует множество систем счислений (двоичные, десятичные, восьмеричные, шестнадцатеричные и т.д.).
Таблица 1- Основания систем счисления.
| q | Название | Цифры |
| двоичная | 0, 1 | |
| троичная | 0, 1, 2 | |
| восьмеричная | 0,..., 7 | |
| шестнадцатеричная | 0,...,9,A, ..., F |
Каждая СС имеет свои правила арифметики (таблица умножения, сложения). Поэтому, производя какие-либо операции над числами, надо помнить о СС, в которой они представлены.
Если основание системы превышает 10, то цифры, начиная с 10, при записи обозначают прописными буквами латинского: A,B,...,Z. При этом цифре 10 соответствует знак «A», цифре 11 - знак «B» и т.д.
Способ записи чисел называют нумерацией или системой счисления.
Система счисления- это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения.
Символы, при помощи которых записывается число, называются цифрами. Следует различать понятия «вид цифры» и «значение цифры».
Системы счисления в зависимости от способа изображения чисел делятся на позиционные и непозиционные.
Системы счисления, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число, называются позиционными.
Системы счисления, в которых каждой цифре соответствует величина, не зависящая от местонахождения этой цифры в записи числа, называются непозиционными.
Система счисления — это совокупность приемов и правил, по которым числа записываются и читаются. Систему счисления образует совокупность правил и приемов представления чисел с помощью набора знаков (цифр).
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число. Например, в числе 757, 7 -первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
В непозиционных системах счисления вес цифры (т. е. тот вклад, который она вносит в значение числа) не зависит от ее позиции в записи числа. Так, в римской системе счисления в числе ХХХII (тридцать два) вес цифры Х в любой позиции равен просто десяти.
Пример. Позиционная система счисления - арабская десятичная система, в которой основание Р= 10 , для изображения чисел используются 10 цифр .
Рассмотрим три числа: 298, 829, 982.
Эти числа различны, хотя в их записи используются одни и те же цифры. 2,8,9. И в каждом числе цифра несет определенный вес в зависимости от того , где она стоит.
В первом числе 2-это сотни.
Во втором - 2 это десятки.
В третьем - 2 это единицы.
В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе.
Пример. Непозиционная система счисления –римская, в которой для каждого числа используется специфическое сочетание символов ( XIV, XXII).
Совокупность различных цифр, используемых в позиционной системе счисления для записи чисел, называется алфавитом системы счисления.
Базис позиционной системы счисления - это последовательность чисел, каждое из которых задаёт значение цифры «по месту» или вес каждого разряда.
Пример базисов традиционных систем:
Десятичная: 10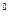 , 10,
, 10,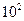 ,10
,10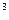 ,….,
,…., 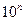
Двоичная: 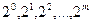
В более общем виде для позиционных систем счисления базис можно записать в виде последовательных членов геометрической прогрессии:
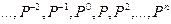 …
…
Знаменатель Р геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основанием системы.
Основание позиционной системы счисления — количество различных цифр, используемых для изображения чисел в данной системе счисления.
За основание системы можно принять любое натуральное число — два, три, четыре и т.д. Следовательно, возможно бесчисленное множество позиционных систем: двоичная, троичная, четверичная и т.д.
При N=2 число различных цифр, используемых для записи чисел, ограничено множеством из двух цифр (нуль и единица). Кроме двоичной системы счисления широкое распространение получили и производные системы:
- двоичная- {0,1};
- десятичная, точнее двоично-десятичное представление десятичных чисел, - {0, 1,...,9};
- шестнадцатеричная - {0,1,2, ...9, А, В, С, D, Е, F}. Здесь шестнадцатеричная цифра А обозначает число 10,В-число 11, ...,F-число 15;
- восьмеричная (от слова восьмерик) - {0,1,2,3,1,5, б, 7}. Она широко используется во многих специализированных ЭВМ.
Восьмеричная и шестнадцатеричная системы счисления являются производными от двоичной, так как 16 = 24 и 8 = 23. Они используются в основном для более компактного изображения двоичной информации, так как запись значения чисел производится существенно меньшим числом знаков.
Как было сказано ранее, в компьютере в двоичном виде может храниться числовая, текстовая, графическая и звуковая информация.
Все числовые данные хранятся в машине в двоичном виде, т.е. в виде последовательности нулей и единиц, однако формы хранения целых и действительных чисел различны.
Целые числа хранятся в форме с фиксированной запятой, действительные числа хранятся в форме с плавающей запятой.
Отметим, что необходимость различного представления целых и действительных чисел вызвана тем, что скорость выполнения арифметических операций над числами с плавающей запятой существенно ниже скорости выполнения этих же операций над числами с фиксированной запятой. Существует большой класс задач, в которых не используются действительные числа. Например, задачи экономического характера, при решении которых данными служат количество деталей, акций, сотрудников и т.д., работают только с целыми числами.
Для решения математических и физических задач, в которых невозможно обойтись только целыми числами, используется представление в форме с плавающей запятой.
Более того, в современных персональных компьютерах процессоры выполняют операции только над целыми числами в форме с фиксированной запятой.
Десятичная система счисления
Основание данной системы равно 10: 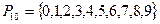
Распишем натуральное число 1578 по следующей схеме:
1 5 7 8
четыре тысячи + пятьсот + семьдесят + восемь
1*1000 + 5*100 + 7*10 + 8
1578 = 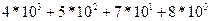
В каждом слагаемом присутствует в качестве множителя степень с основанием 10. Число 10 принято за основание используемой человеком системы счисления. Другими словами, обычно для работы с числами мы используем десятичную систему счисления.
Основание данной системы равно 2: 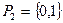
Десятичная система счисления неудобна для использования в электронных машинах. Техническая реализация устройств для операций с десятичными числами является громоздкой и неудобной . В современной вычислительной технике информация кодируется с помощью последовательности сигналов вида : включено или выключено., высокое напряжение или низкое.
Отключено - 0 или низкое напряжение- 0
Включено - 1 или высокое напряжение- 1
Определение. Система счисления с основание Р= 2 , в котором используются всего 2 цифры (0 и 1) , называется двоичная система счисления или бинарная.
Такое кодирование называется двоичным кодирование, а цифры 0 и 1 называются битами.
В ЭВМ каждому символу соответствует последовательность из 8 нулей и единиц, называемая байтом. 1 байт = 8 битов.
Всего существует 256 разных последовательностей из 8 нулей и единиц, это позволяет закодировать 256 различных символов. 2 = 256.
Компьютеры используют двоичную систему потому, что она имеет ряд преимуществ перед другими системами:
- для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.), а не, например, с десятью, — как в десятичной;
- представление информации посредством только двух состояний надежно и помехоустойчиво;
- возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
- двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Общение с компьютером на языке двоичных чисел слишком неудобно. Длинные десятичные числа при переводе в двоичную систему записываются в виде длинных записей (сотни и тысячи нулей и единиц), что делает неудобным работу с такими записями. Мало того, что на эту работу уйдет много времени, но гораздо больше придется потратить на поиск и исправление неизбежных ошибок.
Для облегчения работы с двоичными числами стали использовать в качестве вспомогательного средства систему счисления с основанием 16. Для записи шестнадцатеричных чисел необходимо 16 цифр. Первые десять цифр – это арабские цифры, а остальные шесть цифр – это первые буквы латинского алфавита.
Электронной машине удобно работать с числами, записанными с помощью только двух цифр, т.е. в двоичной системе счисления. Но чтобы человек, работающий с десятичной системой, и компьютер, работающий с двоичной, “понимали” друг друга, необходимо уметь переводить десятичную запись в двоичную и наоборот.
Полезно запомнить запись в этих системах счисления первых двух десятков целых чисел.
Таблица 2 – Представление чисел в разны хсистемах счисления.
| 10-я | 2-я | 8-я | 16-я | 10-я | 2-я | 8-я | 16-я |
| A | |||||||
| B | |||||||
| C | |||||||
| D | |||||||
| E | |||||||
| F | |||||||
Рассмотрим основные алгоритмы преобразование целых чисел из десятичной системы счисления в другую (отличную от десятичной ).
Алгоритм 1. Алгоритм перевода целого числа из десятичной системы счисления в двоичную.
1) делим исходное число а на 2 нацело в десятичной системе и записываем в качестве нового значения десятичного числа а целую часть результата от деления;
2) остаток от деления (это будет 0 или 1) приписываем слева к полученным ранее цифрам в двоичной записи числа а (первая полученная цифра соответствует младшему разряду и ее мы просто записываем);
3) выполняем (1) и (2) до тех пор, пока число а не станет равным 0.
Примеры реализации Алгоритма 1.
Пример1. Переведем число из десятичной системы в 2 – ичную систему.
35610 → х {0;1}
| -3 | ||||||||
| -16 | ||||||||
| -14 | -8 | |||||||
| -18 | -4 | |||||||
| -16 | - 8 | -2 | ||||||
| - 4 | -10 | |||||||
| - 2 | - 4 | |||||||
| -2 | ||||||||
Ответ. 35610 = 1011001002
Пример 2. Переведем число из десятичной системы в 2 – ичную систему.
15110 → х {0;1}
Ответ 15110 = 100101112
Алгоритм 2.Аналогичным образом производится перевод чисел из десятичной системы счисления в любую Р-ичную
Примеры перевода чисел из десятичной системы в любую Р-ичную.
35610 ® Х16
35610=16416
5710→Х7
5710=1117
72610=Х16
72610 = 2D5(16)
Алгоритм 3.Алгоритм перевода целых чисел из Р-ичной системы счисления в десятичную:
1) каждая цифра числа в Р-ичной системы счисления переводится в число в десятичной системе;
2) полученные числа нумеруются справа налево, начиная с нуля (номера соответствуют степеням Р в многочлене;
3) десятичное число, соответствующее каждой Р-ичной цифре, умножается на Pk, где k — номер этого числа, и результаты складываются, причем все эти арифметические действия проводятся в десятичной системе.
Примеры реализации алгоритма.

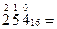
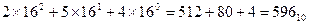


Алгоритм 4. Перевода чисел из двоичной системы в восьмеричную или шестнадцатеричную
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
При переводе двоичной записи в шестнадцатеричную пользуются таблицей 2.
Пример 1: Записать число 111011010011102 в шестнадцатеричной системе счисления.
Решение: Разобьем справа налево данное двоичное число на группы по четыре цифры, приписав впереди, если нужно, незначащие нули. Затем используя таблицу (2), заменим на соответствующие шестнадцатеричные цифры.
Ответ: 11 1011 0100 1110 = 3B1E16
Пример 2: Записать число 13C9A 16 в двоичной системе счисления.
Решение: Используя таблицу , заменим каждую цифру данного шестнадцатеричного числа соответствующими наборами двоичных цифр.
Ответ: 13C9A16 = 0001 0011 1100 1001 10102 = 1 0011 1100 1001 10102
Алгоритм 5.Алгоритм получения дополнительного кода. Перевод отрицательного числа.
Для получения дополнительного k-разрядного кода отрицательного числа необходимо:
1) модуль числа представить прямым кодом в k двоичных разрядах;
2) значения всех бит инвертировать (все нули заменяются на единицы, а единицы на нули), таким образом получается k-разрядный обратный кодисходного числа;
3) к полученному обратному коду, трактуемому как k-разрядное неотрицательное двоичное число, прибавить единицу.
Пример. Перевести отрицательное число в 2-ую систему исчисления.

1100001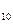 -Прямой код числа
-Прямой код числа
0011110-Обратный код числа
 + 1
+ 1
0011111 – Дополнительный код числа
– Дополнительный код числа
Пример. Найти прямые, обратные и дополнительные коды чисел: -5310.
110112 – прямой код числа.
001002 – обратный код числа.
+
1
(00)1012 – дополнительный код числа.
Алгоритм 6.Алгоритм перевода правильной конечной десятичной дроби в Р-ичную систему счисления:
1) умножим исходное число на Р (основание новой системы счисления), целая часть полученного произведения является первой цифрой после запятой в искомом числе (целая часть может быть как равна нулю, так и быть больше девяти, но она всегда меньше чем Р, это позволяет записать ее в виде ровно одной цифры Р-ичной системы счисления);
2) дробную часть произведения снова умножим на Р, целую часть полученного числа заменяем на цифру в Р-ичной системе и приписываем ее справа к результату;
3) выполняем пункт (2) до тех пор, пока дробная часть произведения не станет равной нулю, или не выделится период (дробная часть окажется равной уже получавшейся ранее дробной части произведения).
Пример. Перевести дробь в 2-ую систему исчисления и назад.
а)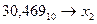
0,469 2 2
| ||||||
0,938 2 2
| ||||||
0,876 2 2
| ||||||
0,752 2 2
| ||||||
0,504 2 2
| ||||||
 0,008 0,008 2 2
| ||||||
11110,011110


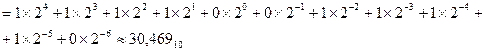
б)
 0,375 0,375 2 2
| ||||||||||||
0,75 2 2
| ||||||||||||
0,5 2 2
| ||||||||||||
1001000000,011
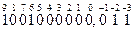

Рассмотрим правила двоичной арифметики через нижеприведённые примеры.
| + | ||||||
а)
| + | |||||||||
б)
| - | |||||||||
в)
| * | |||||||
| + | |||||||
| + | |||||||
г)
| - | , | |||||||||||
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||