Распределенность терминов в суждениях. Круговые схемы отношений между терминами
В логических операциях с суждениями часто возникает необходимость выяснить, распределены ли его термины – субъект и предикат. При этом термин считается распределенным, если его объем полностью включен в объем другого термина, или же
полностью исключается из него. Термин считается нераспределенным, если его объем лишь частично входит в объем другого термина, или же частично из него исключается.
Это следует разъяснить на примере четырех выделенных видов суждений:
Так, в суждениях А – общеутвердительных (Все S есть Р), например, «Все слоны –
животные» субъект распределен, а предикат - нет:

Субъект здесь распределен потому, что его объем полностью включен в объем предиката.
Предикат же не распределен потому, что в нем мыслится только часть животных, совпадающих со слонами.
В суждениях Е – общеотрицательных (Ни одно S не есть Р), например, «Ни один человек не дышит жабрами», и субъект и предикат распределены, т.е. взяты в полном объеме.

В суждениях I – частноутвердительныхкак, например, в суждении «Некоторые студенты нашей группы досрочно сдали все экзамены», S не распределен, так как в нем мыслится только часть студентов, объем S лишь частично включен в объем предиката.
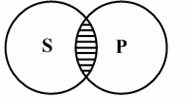
О – частноотрицательные (Некоторые S не есть Р), например, «Некоторые студенты не изучают логику». Субъект здесь не распределен, так как речь идет лишь о части студентов, предикат же распределен, так как в нем мыслятся все изучающие логику, и ни один из них не включен в ту часть студентов, которые мыслятся в субъекте.

Сложное суждение и его виды. Таблица истинности сложных суждений.
Если в структуре простого суждения различают в качестве терминов S и Р, то в сложном суждение может быть несколько субъектов или предикатов. Таким образом, сложное суждение это такое суждение, которое состоит их нескольких простых. При этом важно отметить, что подобно тому, как сложное предложение строится из простых предложений с помощью союзов, так и сложное суждение образуется из простых суждений с помощью логических связок.
Такими логическими связками являются: конъюнкция, дизъюнкция, импликация, эквиваленция и отрицание.
Сложное конъюнктивное, или соединительное, суждение состоит из двух или более простых суждений, соединенных между собой логической связкой конъюнкцией. В естественном языке конъюнкции соответствует соединительный союз - «и», а также союзы «да», «а», «но», «хотя», «однако», взятые в значении «и». Для обозначении конъюнкции в логике используют значки
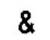

Сложное дизъюнктивное, или разделительное, суждение состоит из простых суждений, соединенных логической связкой дизъюнкцией, которой в естественном языке соответствуют союзы «или», «либо». Можно говорить о двух разновидностях дизъюнкции: слабой (не исключающей) и строгой (исключающей). Для слабой дизъюнкции характерно употребление союзов «или» / «либо» в соединительно-разделительном смысле - или то, или другое, или то и другое вместе. Слабая дизъюнкция обозначается значком:

Что касается сильной дизъюнкции, то для нее характерно употребление союзов «или» / «либо» в исключающее-разделительном смысле – или то, или другое, но не то и другое вместе. Обозначается она, как и слабая дизъюнкция, но с точкой наверху.
Сложное импликативное, или условное суждение образуется из двух простых с помощью логической связки импликации, которой в естественном языке соответствует союз «если…, то…». Символически импликацию обозначают следующим образом:
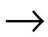
Суждения эквиваленции – это сложные суждения, состоящие из простых суждений, соединенных логической связкой эквиваленции, которой в естественном языке соответствуют следующие союзы: «если и только если», «тогда и только тогда, когда»
. Символически эквиваленция записывается с помощью тройного равенства
Таблица истинности сложных суждений.Истинность или ложность простых суждений проверяется обычно их сопоставлением с реальным положением дел;
