Дифференциальные уравнения высших порядков, допускающие понижение порядка.

Порядком дифференциального уравнения называют наивысший порядок содержащихся в нем производных.

Пример 1. 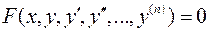дифференциальное уравнение -го порядка.

1 Тип. Уравнение вида .

Общее решение находится путём n кратного интегрирования.

2 тип. Уравнение вида , то есть не содержащее явно аргумент х.

Общее решение находится путём понижения на единицу порядка уравнения. Используется правило дифференцирования:

3 тип. Уравнение вида , то есть не содержащее явно искомую функцию.

Общее решение находится путём понижения порядка уравнения.

.

Примеры.

- дифференциальное уравнение четвертого порядка, допускающее понижение порядка.

- дифференциальное уравнение третьего порядка не содержащее явно аргумент х, допускающее понижение порядка.

- дифференциальное уравнение второго порядка не содержащее явно искомую функцию.