Дифференциальные уравнения второго порядка. Однородные дифференциальные уравнения второго порядка.
Дифференциальное уравнение вида называется дифференциальным уравнением второго порядка..
называется дифференциальным уравнением второго порядка..
Общее решение уравнения зависит от двух неопределенных постоянных  и
и  и записывается в форме
и записывается в форме 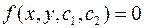 . Задача Коши для дифференциального уравнения второго порядка решается при начальных условиях:
. Задача Коши для дифференциального уравнения второго порядка решается при начальных условиях:
 .
.
Если дифференциальное уравнение второго порядка не содержит какой-либо из величин 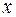 или
или 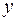 , то оно называется неполным.
, то оно называется неполным.
Алгоритм решения.
Преобразовать в дифференциальное уравнение первого порядка путем введения новой переменной 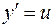 .
.
Пример. 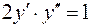 - неполное дифференциальное уравнение второго порядка.
- неполное дифференциальное уравнение второго порядка.
Найти частное решение уравнения 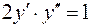 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям: 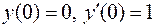 -задача Коши для дифференциального уравнения второго порядка.
-задача Коши для дифференциального уравнения второго порядка.
Уравнение вида 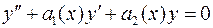 , (1)
, (1)
называют однородным уравнением.
Однородное уравнение обладает тем свойством, что, если 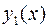 и
и 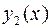 являются его частными решениями, то выражение
являются его частными решениями, то выражение  (2) также будет решением данного уравнения при произвольных значениях постоянных
(2) также будет решением данного уравнения при произвольных значениях постоянных  и
и  .
.
Уравнение вида  (3) называется однородным уравнением с постоянными коэффициентами
(3) называется однородным уравнением с постоянными коэффициентами
Алгоритм решения.
1. Составляем характеристическое уравнение  .
.
2. Решая квадратное уравнение, будем иметь
 . (4)
. (4)
Возможны варианты решения:
1.  .
.
В этом случае выражение (4) определяет два различных значения  и
и  . Общее решение уравнения запишем в виде:
. Общее решение уравнения запишем в виде:
 . (5)
. (5)
2.  .
.
Теперь квадратное уравнение имеет только один корень  .
.
Общее решение однородного уравнения запишется в форме
 . (6)
. (6)
3.  .
.
Квадратное уравнение имеет комплексные корни  и
и  .
.
Общее решение однородного уравнения будет
 . (7)
. (7)
Примеры.  ,
,  ,
,  однородные уравнения с постоянными коэффициентами.
однородные уравнения с постоянными коэффициентами.
Замечание. Задача Коши для однородных дифференциальных уравнений с постоянными коэффициентами всегда имеет единственное решение.