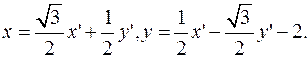Формулы преобразования координат

8.1. Рассмотрим на плоскости две аффинные системы координат:

(старая и новая системы координат).

Пусть точка и

Задача преобразования координат состоит в

следующем: выразить старые координаты

точки через новые

Зададим систему относительно

(1)

 

По правилу треугольника получим: или (используем (1))

 

(2)

Формулы (2) называются формулами преобразования координат.

Заметим, что матрица перехода от базиса к базису в точности совпадает с матрицей из коэффициентов при

в формулах (2). Определитель этой матрицы поэтому система (2) разрешима относительно

Интересны два частных случая.

(А) Перенос начала.

(В) Замена координатных векторов.

Пример.Написать формулы преобразования координат в аффинной системе, если

∆ ▲

 

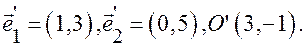
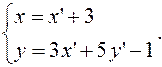8.2. Рассмотрим преобразование прямоугольных координат. Дпск есть частный случай аффинной системы, поэтому можно использовать формулы (2). На коэффициенты матрицы перехода С накладываются определенные условия.

Возможны два случая.

С) Системы 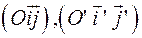ориентированы одинаково (обе правые).

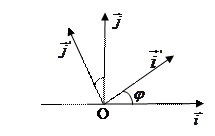
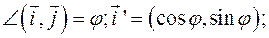
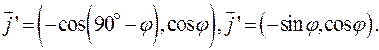
Формулы (2) запишутся так:

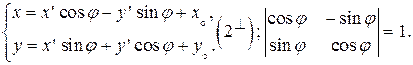
D) Системы 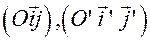ориентированы противоположно.

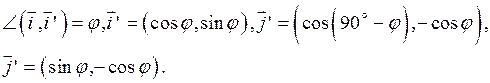
Формулы (2) запишутся так:

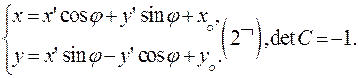
Объединим Формулы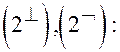

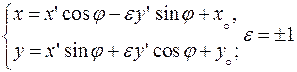. (3)

(«+» для одинаково ориентированных систем).

Задача.Определите координаты новых векторов и нового начала, если формулы преобразования имеют вид:

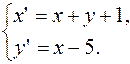отв.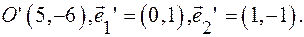

Задача.Напишите формулы преобразования прямоугольных декартовых координат, если 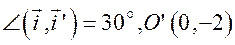и системы 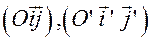одинаково ориентированы.

Отв.