Первообразная и неопределенный интеграл.
no1. Понятие первообразной и неопределенного интеграла. Пусть функция  определена на некотором конечном или бесконечном промежутке
определена на некотором конечном или бесконечном промежутке  .
.
Определение 1. Дифференцируемая на промежутке  функция
функция  называется первообразной функции
называется первообразной функции  на этом промежутке, если
на этом промежутке, если  .
.

| (1) |
Замечание 1. Первообразная  функции
функции  на промежутке
на промежутке  ,будучи дифференцируемой функцией на этом промежутке является также и непрерывной на нем.
,будучи дифференцируемой функцией на этом промежутке является также и непрерывной на нем.
Замечание 2. Очевидно, если  - первообразная функции
- первообразная функции  на промежутке
на промежутке  , то какова бы ни была постоянная
, то какова бы ни была постоянная  , функция
, функция
 (
(  ) также является первообразной для
) также является первообразной для  :
:
 
|
Более того, как показывает следующая простая теорема любые две первообразные функции  на промежутке
на промежутке  ,отличаются друг от друга на этом промежутке на некоторую постоянную.
,отличаются друг от друга на этом промежутке на некоторую постоянную.
Теорема 1. Если  и
и  - две первообразные функции
- две первообразные функции  на промежутке
на промежутке  , то существует такая постоянная
, то существует такая постоянная  что
что
 
|
Д о к а з а т е л ь с т в о. Так как  и
и  – первообразные функции
– первообразные функции  на промежутке
на промежутке  , то
, то
 и и   . .
|
Поэтому
 
|
но это, как известно, означает, что функция  является постоянной на промежутке
является постоянной на промежутке  □
□
Таким образом, если  - какая то первообразная функции
- какая то первообразная функции  то любая другая имеет вид
то любая другая имеет вид  , где
, где  некоторая постоянная.
некоторая постоянная.
Определение 2. Совокупность всех первообразных функции  на промежутке
на промежутке  называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  .
.
Неопределенный интеграл от функции  обозначается следующим образом
обозначается следующим образом
 , ,
|
при этом символ  называется знаком интеграла, а функция
называется знаком интеграла, а функция  - подынтегральной функцией .
- подынтегральной функцией .
Если  какая то первообразная функции
какая то первообразная функции  на данном промежутке
на данном промежутке  , то в соответствии с теоремой 1 совокупность всех первообразных функции
, то в соответствии с теоремой 1 совокупность всех первообразных функции  есть следующее множество функций:
есть следующее множество функций:

|
Таким образом, по определению неопределенного интеграла
  
| (2) |
Однако обычно пишут короче:
 . .
| (3) |
где  - произвольная постоянная.
- произвольная постоянная.
Замечание 3. В связи с определением неопределенного интеграла отметим, что равенство двух неопределенных интегралов

|
это – равенство двух множеств, а именно, множеств первообразных функций  и
и 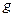 . Последнее следует иметь в виду ниже, когда будут рассматриваться свойства неопределенного интеграла.
. Последнее следует иметь в виду ниже, когда будут рассматриваться свойства неопределенного интеграла.
Отметим еще, что если  - первообразная функции
- первообразная функции  , то
, то

|
В связи с этим далее по определению будем считать , что

|
no 2. Основные свойства неопределенного интеграла.
 . Если функция
. Если функция  дифференцируема на промежутке
дифференцируема на промежутке  , то
, то

|
или, иначе,
 . .
|
 . Если функция
. Если функция  имеет первообразную , то
имеет первообразную , то

|
и, следовательно,
 . .
|
Свойства  и
и  являются прямыми следствиями определения 2 . Они показывают, что в некотором смысле операции интегрирования и дифференцирования являются обратными друг другу.
являются прямыми следствиями определения 2 . Они показывают, что в некотором смысле операции интегрирования и дифференцирования являются обратными друг другу.
 . Если функция
. Если функция  имеет первообразную, то какова бы ни была постоянная
имеет первообразную, то какова бы ни была постоянная  , функция
, функция  также имеет первообразную, причем всякая первообразная функции
также имеет первообразную, причем всякая первообразная функции  равна произведению числа
равна произведению числа  на некоторую первообразную функции
на некоторую первообразную функции  и, наоборот, всякое такое произведение есть некоторая первообразная функции
и, наоборот, всякое такое произведение есть некоторая первообразная функции  , т.е.
, т.е.

|
Таким образом, постоянную можно выносить за знак неопределенного интеграла.
 . Если функции
. Если функции  и
и  имеют первообразные на промежутке
имеют первообразные на промежутке  ,то и функция
,то и функция  имеет на нем первообразную , причем всякая первообразная функции
имеет на нем первообразную , причем всякая первообразная функции  является суммой некоторых первообразных функций
является суммой некоторых первообразных функций  и
и  ; верно и обратное : всякая такая сумма является первообразной функции
; верно и обратное : всякая такая сумма является первообразной функции  .Таким образом,
.Таким образом,

|
Упражнение 1. Приведите доказательства свойств  и
и  неопределенного интеграла.
неопределенного интеграла.
Следствием свойств  и
и  являются следующее свойства:
являются следующее свойства:
 . (Линейность неопределенного интеграла ). Если функции
. (Линейность неопределенного интеграла ). Если функции  и
и  имеют первообразные на промежутке
имеют первообразные на промежутке  , то каковы бы не были вещественные числа
, то каковы бы не были вещественные числа  и
и  , функция
, функция  также имеет первообразную на промежутке
также имеет первообразную на промежутке  , причем
, причем
 
|
Замечание 4. Свойства  и
и  неопределенного интеграла естественным образом распространяются на любое конечное число функций
неопределенного интеграла естественным образом распространяются на любое конечное число функций  , имеющих первообразные на промежутке
, имеющих первообразные на промежутке  .В частности для любых постоянных
.В частности для любых постоянных 

|
Справедливость этого неравенства легко установить индукцией по  .
.
no3. Таблица неопределенных интегралов от элементарных функций. Для того ,чтобы найти первообразную функции  , а следовательно и неопределенный интеграл от этой функции, нужно найти такую функцию
, а следовательно и неопределенный интеграл от этой функции, нужно найти такую функцию  , производная которой
, производная которой  всюду на заданном промежутке совпадает с функцией
всюду на заданном промежутке совпадает с функцией  . Поэтому из таблицы для производных вытекает следующая таблица неопределенных интегралов.
. Поэтому из таблицы для производных вытекает следующая таблица неопределенных интегралов.
| 1. | 
|
| 2. | 
|
| 3. | 
|
| 4. | 
|
| 5. | 
|
| 6. | 
|
| 7. | 
|
| 8. | 
|
| 9. | 
|
| 10. | 
|
| 11. | 
|
| 12. | 
|
| 13. | 
|
| 14. | 
|
Полезно помнить также , что имеют место и следующие две формулы:
| 15. | 
|
| 15. | 
|
Упражнение 2. Докажите справедливость двух последних формул.
no4. Формула интегрирования по частям и формула замены переменной в неопределенном интеграле.
Теорема 2. Пусть функции  и
и  дифференцируемы на промежутке
дифференцируемы на промежутке  и существует первообразная функции
и существует первообразная функции  .
.
Тогда существует и первообразная функции  ,а также имеет место формула
,а также имеет место формула

| (1) |
(формула интегрирования по частям).
Д о к а з а т е л ь с т в о. По правилу дифференцирования произведения дифференцируемых функций имеет место формула
 . .
|
Запишем её в виде

|
По условию функция  имеет первообразную; функция
имеет первообразную; функция  также имеет первообразную (ей является функция
также имеет первообразную (ей является функция  ). Поэтому в силу свойства линейности неопределенного интеграла из предыдущего равенства следует, что первообразную имеет и функция
). Поэтому в силу свойства линейности неопределенного интеграла из предыдущего равенства следует, что первообразную имеет и функция  , причем
, причем
  □ □
|
Замечание 5.При выводе последней формулы мы воспользовались очевидным равенством

|
Замечание 6.Формулу интегрирования по частям часто записывают в виде

|
или, короче,

|
Теорема 3. Пусть функция  имеет первообразную
имеет первообразную  на промежутке
на промежутке  , а функция
, а функция  дифференцируема на промежутке
дифференцируема на промежутке  и
и  . Тогда
. Тогда

| (2) |
Д о к а з а т е л ь с т в о. Достаточно доказать , что  - первообразная подынтегральной функции.
- первообразная подынтегральной функции.
По условию
 . .
|
Поэтому по правилу дифференцирования сложной функции имеем
 □ □
|
Замечание 7.Формулу (2) можно записать в виде
 ,
,
а следовательно и в каждой из следующих двух равносильных форм:

| (2’) |
или
 , ,
| (2”) |
где  . Каждую из этих двух равносильных формул называют формулой замены переменной (по правилу
. Каждую из этих двух равносильных формул называют формулой замены переменной (по правилу  ).
).