Производная и ее геометрический и физический смысл.

n°1. Понятие производной.

Пусть и . Точка называется внутренней точкой множества , если она принадлежит ему вместе с некоторой своей окрестностью, т.е. существует такая окрестность точки , что .

Пусть теперь функция определена на множестве и - внутренняя точка множества .Тогда существует такая окрестность точки , что и, следовательно, функция

определена на множестве 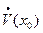и – точка сгущения этого множества. Таким образом, корректно следующее

Определение 1. Если существует предел

то он называется производной функции в точке .

Производная функции () в точке обозначается одним из следующих символов:

, , , ,

при этом если ясно, в какой точке рассматривается производная, то для ее обозначения используют символы: , , , .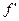

Таким образом,

(1)

Замечание 1: Если положить , , то теорема о пределе суперпозиции позволяет также определить производную с помощью любого из равенств:

(2)

(3)

Величины и называют, соответственно, приращением аргумента и приращением функции в точке . В соответствии с равенством (3), можно сказать, что производная равна пределу отношения приращения функции (в точке ) к приращению аргумента.

Замечание 2: Определение производной выше было дано в предположении, что точка - внутренняя точка области определения функции . Если же точка не является внутренней точкой множества , но принадлежит этому множеству вместе с некоторой своей односторонней окрестностью , или , то можно ввести понятие односторонней производной:

(правая производная)

(левая производная).

Замечание 3: Если предел (1) равен или , то производная называется бесконечной.

Теорема 1.Пусть функция определена в окрестности точки и имеет в этой точке конечную производную. Тогда она непрерывна в этой точке.

Д о к а з а т е л ь с т в о. Достаточно заметить, что

□

§2. Дифференцируемые функции. Понятие дифференциала и его геометрический и физический смысл.

Пусть функция определена в окрестности точки .

Определение 1. Если существует такая линейная функция вещественного аргумента (), что приращение функции может быть представлено в виде

(1)

где - бесконечно малая при высшего порядка по сравнению с функцией (т.е. при ), то функция называется дифференцируемой в точке , а соответствующая линейная функция называется ее дифференциалом в этой точке.

Дифференциал функции в точке обычно обозначается одним из символов:

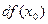или .

В последнем случае имеют в виду, что , при этом часто опускают указание о том, в какой точке рассматривается этот дифференциал, т.е. для обозначения дифференциала используют символы или . Таким образом,

(2)

Замечание 1: Очевидно, равенство (1) можно записать в виде

(1’)

где , или, короче, в виде

(1’’)

где - приращение функции в точке , соответствующее приращению аргумента . Поэтому вместо (2) также пишут:

(2’)

т.е. трактуют аргумент в (2) как переменное приращение аргумента функции в точке .

Теорема 1. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную .

Д о к а з а т е л ь с т в о. Необходимость. Пусть функция дифференцируема в точке . Тогда из равенства (1) следует, что

Это означает, что существует конечная производная

Достаточность. Предположим, что в точке функция имеет конечную производную . Тогда из равенства

следует, что

(3)

где 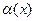- бесконечно малая при функция. Поэтому

(4)

и так как

(ибо ),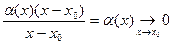

то равенство (4) можно записать в виде:

(5)

т.е. в виде (1), где . Таким образом, функция дифференцируема в точке . □

Замечание 2: С учетом доказательства теоремы можно утверждать, что дифференциал функции в точке есть следующая линейная функция от приращения аргумента :

(6)

А поскольку для функции имеем 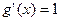, то

т.е.

то можно сказать, что- - дифференциал независимой переменной и, следовательно, определению дифференциала 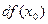можно придать форму:

(7)

Отсюда, в частности, становится понятным, почему для обозначения производной используют также обозначение .

Геометрический смысл дифференциала: Нетрудно убедиться, что значение дифференциала в точке равно приращению ординаты касательной к графику функции в точке . Подробнее об этои см. учебники Фихтенгольца и Кудрявцева.

Физический смысл дифференциала: Если – длина пути, проходимого материальной точкой за время , то дифференциал (– скорость в момент времени ) – путь, который она бы прошла за промежуток времени при условии, что она бы двигалась на нем с постоянной скоростью, равной скорости в момент времени . Если 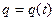– количество электричества, протекающее через поперечное сечение проводника в момент времени , то дифференциал (– сила тока в момент времени ) – количество электричества, которое протекло бы через это поперечно сечение за время , точнее от момента времени до момента времени , при условии, что сила тока была бы постоянной и равнялась силе тока в момент времени .

§3. Арифметические операции с дифференцируемыми функциями.

Теорема. Пусть функции и определены в окрестности точки и дифференцируемы в этой точке. Тогда в этой точке дифференцируема и каждая из функций

, , и (при ),

причем

(1)

(2)

(3)

(4)

Д о к а з а т е л ь с т в о: 1. Дифференцируемость функции и равенство (1) очевидно будут установлены, если будут установлены дифференцируемость функции и равенство (3). В последнем случае достаточно будет рассмотреть функцию .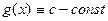

2. Дифференцируемость функции и равенство (2) вытекают из того, что имеют место равенства

и из того, что по условию существуют конечные пределы

и ,

при этом следует помнить, что дифференцируемость функции в точке равносильна существованию конечной ее производной в этой точке.

3. Дифференцируемость произведения функций и равенство (3).

Пусть

Тогда

и, следовательно,

(5)

В силу дифференцируемости функций и в точке , существуют конечные пределы

(6)

Поэтому из (5) следует, что существует конечный предел

(7)

т.е. функция дифференцируема в точке . Переходя в равенстве (5) к пределу при с учетом равенств (6) и (7) получим равенство (3).

4. Дифференцируемость и равенство (4). Положим . По крайней мере, в некоторой окрестности точки , это определение корректно, так как и функция непрерывна в точке .

Далее, имеем:

и, следовательно,

Рассуждая теперь аналогично пункту 3 данного доказательства, убеждаемся, что функция дифференцируема в точке , а переходя здесь к пределу при получим также и равенство (4). □

Замечание (о формулах для дифференциалов, вытекающих из формул (1) - (6)). Учитывая, что дифференциал функции в точке находится по правилу из формул (1)–(4) , умножая каждую из них на , получим следующие формулы для дифференциалов:

(здесь );

;