Бесконечно малые и бесконечно большие функции.
Определение 1. Пусть функция  определена на множестве
определена на множестве 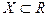 и
и  - его точка сгущения. Функция
- его точка сгущения. Функция 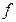 называется бесконечно малой при
называется бесконечно малой при 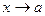 если
если  .
.
Упражнения. 1. Покажите, что  - бесконечно малая функция при
- бесконечно малая функция при  .
.
2. Докажите, что функция 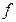 - бесконечно малая при
- бесконечно малая при  в том и только том случае, если функция
в том и только том случае, если функция  - бесконечно малая при
- бесконечно малая при  .
.
Следующая теорема является простым следствием теоремы о пределе суммы.
Теорема 1. Сумма любого конечного числа бесконечно малых при  функций есть бесконечно малая при
функций есть бесконечно малая при  функция.
функция.
Теорема 2.Произведение бесконечно малой при  функции
функции 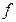 и ограниченной в окрестности точки
и ограниченной в окрестности точки 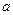 функции
функции  является бесконечно малой при
является бесконечно малой при  функцией.
функцией.
Замечание 1. Точнее в этой теореме предполагается, что функция  ограничена на множестве
ограничена на множестве  , где
, где 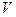 – некоторая окрестность точки
– некоторая окрестность точки 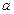 , которая является точкой сгущения множества
, которая является точкой сгущения множества 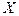 (это же множество, без ущерба для общности, можно считать и областью определения функции
(это же множество, без ущерба для общности, можно считать и областью определения функции 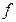 ).
).
С учетом определения предела функции по Гейне, эта теорема является прямым следствием аналогичной теоремы для числовых последовательностей (теоремы о произведении бесконечно малой последовательности на ограниченную последовательность).
Определение 2.Пусть  – точка сгущения множества
– точка сгущения множества 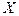 . Функция
. Функция  называется бесконечно большой при
называется бесконечно большой при 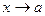 , если
, если  .
.
Теорема 3(о связи между бесконечно малыми и бесконечно большими). Пусть  - точка сгущения множества
- точка сгущения множества  и
и  на
на 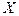 (или, хотя бы, в некоторой окрестности точки
(или, хотя бы, в некоторой окрестности точки 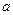 ). Тогда
). Тогда
1) если 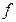 – бесконечно малая при
– бесконечно малая при  функция, то
функция, то  – бесконечно большая при
– бесконечно большая при  функция;
функция;
2) если же 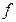 – бесконечно большая при
– бесконечно большая при  функция, то
функция, то  – бесконечно малая при
– бесконечно малая при  функция.
функция.
Д о к а з а т е л ь с т в о. 1) Выберем произвольное  и положим
и положим  . Так как
. Так как  , то найдется такая окрестность
, то найдется такая окрестность 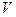 точки
точки 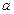 , что
, что

и, следовательно,  . В силу произвольности
. В силу произвольности  это и означает, что
это и означает, что  – бесконечно большая при
– бесконечно большая при  функция.
функция.
2) Возьмем произвольное  и положим
и положим  . Поскольку
. Поскольку  , то найдется такая окрестность
, то найдется такая окрестность  точки
точки 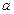 , что
, что
 ,
,
Поэтому  , т.е. то
, т.е. то  – бесконечно малая при
– бесконечно малая при  функция □
функция □
§6. Символы «о» и «О». Эквивалентные при функции.
функции.
Пусть функции  и
и  определены на множестве
определены на множестве 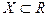 и
и  – точка сгущения множества
– точка сгущения множества 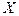 . Пусть также в некоторой проколотой окрестности
. Пусть также в некоторой проколотой окрестности  точки
точки 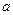 функция
функция  отлична от нуля (точнее,
отлична от нуля (точнее,  ). Там где это ниже необходимо по смыслу, будем также считать, что в той же проколотой окрестности отлична от нуля и функция
). Там где это ниже необходимо по смыслу, будем также считать, что в той же проколотой окрестности отлична от нуля и функция 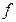 .
.
Определения: 1. Если
 ,
,
то говорят, что функция 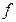 есть о-малое от функции
есть о-малое от функции  при
при 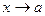 , и пишут
, и пишут
 при
при  .
.
2.Если функция  ограничена в некоторой проколотой окрестности
ограничена в некоторой проколотой окрестности  точки
точки 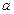 , т.е. если она ограничена на множестве
, т.е. если она ограничена на множестве  , то говорят, что функция
, то говорят, что функция 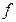 есть о-большое от функции
есть о-большое от функции  при
при  , и пишут
, и пишут
 при
при  .
.
3. Говорят, что функции 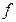 и
и  одного порядка при
одного порядка при  , если
, если
 и
и  при
при  .
.
4.Говорят, что функции 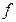 и
и  асимптотически равны при
асимптотически равны при  , если
, если