А. Локальные свойства функций, имеющих предел.
Определение 1.Пусть функция  определена на множестве
определена на множестве 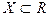 и
и  – некоторое его подмножество (
– некоторое его подмножество ( ). Говорят, что функция
). Говорят, что функция 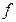 ограничена на множестве
ограничена на множестве  , если его образ
, если его образ  есть ограниченное множество.
есть ограниченное множество.
Замечание 1.Аналогично вводятся понятия ограниченности функции 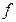 на множестве
на множестве  сверху и снизу.
сверху и снизу.
Замечание 2.Ограниченность функции 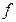 на множестве
на множестве  очевидно означает, что
очевидно означает, что  .
.
Теорема 1 (о локальной ограниченности). Пустьфункция 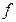 определена на множестве
определена на множестве 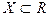 и
и 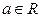 - точка сгущения этого множества. Тогда если существует предел
- точка сгущения этого множества. Тогда если существует предел  , то в некоторой окрестности точки
, то в некоторой окрестности точки 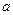 функция
функция 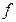 является ограниченной. Точнее, существует такая окрестность
является ограниченной. Точнее, существует такая окрестность 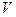 точки
точки 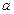 , что функция
, что функция 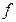 ограничена на множестве
ограничена на множестве  .
.
Д о к а з а т е л ь с т в о. Пусть  и
и  Тогда по определению предела для
Тогда по определению предела для  найдется такая окрестность
найдется такая окрестность  точки
точки 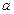 , что
, что

А так как
 ,
,
то

Следовательно функция 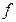 ограничена на множестве
ограничена на множестве  , а тогда она, очевидно,ограничена и на множестве
, а тогда она, очевидно,ограничена и на множестве  □
□
Ниже знак числа  обозначается через
обозначается через  .
.
Теорема 2 (о стабилизации знака). Пустьфункция 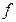 определена на множестве
определена на множестве 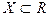 и
и 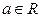 - точка сгущения этого множества. Тогда если существует отличный от нуля предел
- точка сгущения этого множества. Тогда если существует отличный от нуля предел  , то в некоторой проколотой окрестности точки
, то в некоторой проколотой окрестности точки 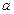 функция
функция 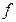 имеет тот же знак, что и этот предел: точнее, существует такая окрестность
имеет тот же знак, что и этот предел: точнее, существует такая окрестность 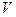 точки
точки 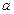 , что
, что

| (1) |
Д о к а з а т е л ь с т в о. Пусть для определенности  .
.
Тогда  - некоторая окрестность точки
- некоторая окрестность точки 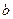 . По определению предела существует такая окрестность
. По определению предела существует такая окрестность 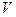 точки
точки 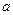 , что
, что  , а по выбору окрестности
, а по выбору окрестности 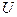 это означает, что
это означает, что  , и, следовательно, имеет место равенство (1) □
, и, следовательно, имеет место равенство (1) □
§ 2б. Предел суперпозиции.
Теорема(о пределе суперпозиции). Пусть функция  определена на множестве
определена на множестве 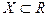 ,
,  – точка сгущения множества
– точка сгущения множества 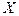 и существует предел
и существует предел
 . .
| (2) |
Пусть, кроме того, функция  определена на множестве
определена на множестве  ,
, 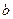 – точка сгущения множества
– точка сгущения множества  и существует предел.
и существует предел.
 . .
| (3) |
Тогда, если  , то на множестве
, то на множестве  имеет смысл суперпозиция
имеет смысл суперпозиция  и существует предел.
и существует предел.
 . .
| (4) |
Д о к а з а т е л ь с т в о. Выберем произвольную окрестность  точки
точки  . Тогда, в силу равенства (3), найдется окрестность
. Тогда, в силу равенства (3), найдется окрестность  точки
точки 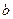 такая, что
такая, что

| (5) |
В свою очередь, в силу равенства (2), для окрестности  точки
точки  найдется такая окрестность
найдется такая окрестность  точки
точки 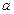 , что
, что
 ,
,
а так как  и по условию
и по условию  , то отсюда следует, что
, то отсюда следует, что
 . .
| (6) |
Из включений (5) и (6) следует, что
 .
.
Таким образом, для произвольно выбранной окрестности  точки
точки  нашлась окрестность
нашлась окрестность  точки
точки 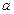 такая, что
такая, что  . По определению предела это и означает, что имеет место равенство (4) □
. По определению предела это и означает, что имеет место равенство (4) □