Критерий Коши существования предела функции.
.
Определение 3(предела по Гейне).Пусть функция 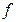 определена на множестве
определена на множестве 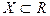 и
и 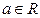 – точка сгущения этого множества. Число
– точка сгущения этого множества. Число  называется пределом функции
называется пределом функции 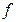 при
при  или, также, пределом функции
или, также, пределом функции 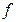 в точке
в точке 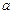 , если для любой последовательности
, если для любой последовательности  последовательность
последовательность  сходится и
сходится и
 . .
| (3) |
Замечание 4.Последнее определение называют также определением предела функции на языке последовательностей.
Теорема 1.Определения предела функции по Коши и по Гейне равносильны.
Д о к а з а т е л ь с т в о. Требуется доказать, что если число  является пределом функции
является пределом функции  при
при 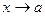 в смысле одного из определений 2 и 3, то оно является также и ее пределом в точке
в смысле одного из определений 2 и 3, то оно является также и ее пределом в точке 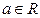 (точке сгущения множества
(точке сгущения множества 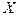 ) и в смысле другого из этих определений.
) и в смысле другого из этих определений.
Пусть
 (в смысле Коши)
(в смысле Коши)
| (4) |
Выберем произвольную последовательность

и произвольное  . В силу условия (4) и определения 2 найдется
. В силу условия (4) и определения 2 найдется  такое, что для любого
такое, что для любого  , удовлетворяющего неравенствам (1) имеет место и неравенство (2). В свою очередь, поскольку
, удовлетворяющего неравенствам (1) имеет место и неравенство (2). В свою очередь, поскольку 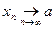 , то для этого
, то для этого  найдется такой номер
найдется такой номер  , что
, что
 ,
,
а так как по условию  и
и 
 , то по определению 2
, то по определению 2
  . .
| (5) |
В силу произвольности  это и означает, что имеет место равенство (3), т.е.
это и означает, что имеет место равенство (3), т.е.
 (в смысле Гейне)
(в смысле Гейне)
| (6) |
Обратно, пусть имеет место равенство (6). Докажем, что тогда имеет место и равенство (4). Предположим противное. Тогда  :
:
 .
.
Зафиксируем это  . Для него, в частности,
. Для него, в частности,  :
:
 ,
,
при этом очевидно, что  . Таким образом, нашлась последовательность
. Таким образом, нашлась последовательность  такая, что
такая, что

| (7) |
Однако, для той же последовательности и того же  в силу условия (6), определения 3 и определения предела числовой последовательности найдется такой номер
в силу условия (6), определения 3 и определения предела числовой последовательности найдется такой номер  , что будет иметь место и неравенство (5), противоречащее неравенству (7). Следовательно (6)⇒(4) □
, что будет иметь место и неравенство (5), противоречащее неравенству (7). Следовательно (6)⇒(4) □
Следующие теоремы, с учетом определения предела функции по Гейне являются прямыми следствиями аналогичных теорем о пределе последовательности.
Теорема 2. Если функция  имеет предел в точке
имеет предел в точке 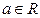 , где
, где 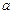 – точка сгущения множества
– точка сгущения множества 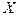 , то этот предел единственный.
, то этот предел единственный.
Теорема 3(об арифметических свойствах предела функции). Пустьфункции  и
и  определены на множестве
определены на множестве 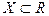 и
и 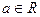 - точка сгущения этого множества. Тогда если существуют пределы
- точка сгущения этого множества. Тогда если существуют пределы
 и
и  ,
,
то существуют и пределы
 ,
,  ,
,  ,
, 
(последний при дополнительном предположении, что и  ),
),
причем
а) 

 ,
,
б) 



 (теорема о пределе суммы и разности),
(теорема о пределе суммы и разности),
в) 


 (теорема о пределе произведения),
(теорема о пределе произведения),
г) 

 (теорема о пределе частного).
(теорема о пределе частного).
Теорема 4 (о предельном переходе в неравенстве). Пустьфункции 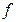 и
и  определены на множестве
определены на множестве 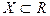 и
и 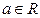 - точка сгущения множества
- точка сгущения множества  . Тогда если
. Тогда если

и существуют пределы и
и  , то
, то


 .
.
Теорема 5(принцип двух милиционеров). Пустьфункции 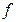 ,
,  и
и  определены на множестве
определены на множестве 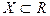 и
и 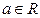 - точка сгущения множества
- точка сгущения множества  . Тогда если
. Тогда если

и существуют равные между собой пределы
 и
и  ,
,
то существует и равный им предел
 ,
,
т.е.




 .
.
Теорема(критерий Коши). Пусть функция 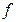 определена на множестве
определена на множестве 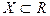 и
и 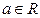 точка сгущения этого множества. Для того, чтобы существовал предел
точка сгущения этого множества. Для того, чтобы существовал предел

| (7) |
необходимо и достаточно, чтобы 


 . .
| (8) |
Д о к а з а т е л ь с т в о. Необходимость. Пусть существует предел (7) и для определенности пусть 
 . Выберем произвольное
. Выберем произвольное  . Тогда найдется такое
. Тогда найдется такое 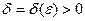 , что для любых
, что для любых  , удовлетворяющих неравенствам
, удовлетворяющих неравенствам  и
и  справедливы неравенства
справедливы неравенства
 и
и  .
.
Поскольку  , то тогда при тех же
, то тогда при тех же  справедливо и неравенство (8). Необходимость доказана.
справедливо и неравенство (8). Необходимость доказана.
Достаточность. Покажем сначала, что для любой последовательности  , последовательность
, последовательность  – фундаментальная и, следовательно, она имеет предел. Выберем произвольную последовательность
– фундаментальная и, следовательно, она имеет предел. Выберем произвольную последовательность  и произвольное
и произвольное  . По условию
. По условию  такое, что
такое, что  справедливо неравенство (8). Зафиксируем это
справедливо неравенство (8). Зафиксируем это  . Тогда в силу того, что
. Тогда в силу того, что  и
и  найдется такой номер
найдется такой номер  , что при
, что при 
 .
.
Таким образом,  при
при  , но тогда по выбору
, но тогда по выбору  имеем
имеем
 .
.
В силу произвольности выбранного  это и означает, что последовательность
это и означает, что последовательность  – фундаментальная.
– фундаментальная.
Покажем теперь, что для любой последовательности  предел
предел  один и тот же. Тогда в силу определения предела функции по Гейне это и будет означать, что существует предел (7). Предположим противное, т.е. пусть имеются две последовательности
один и тот же. Тогда в силу определения предела функции по Гейне это и будет означать, что существует предел (7). Предположим противное, т.е. пусть имеются две последовательности  и
и  (
( ), которые сходятся к точке
), которые сходятся к точке 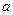 и
и  ,
,  , причем
, причем  . Рассмотрим последовательность
. Рассмотрим последовательность
 .
.
Очевидно, она сходится к точке 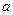 , при этом все ее точки принадлежат множеству
, при этом все ее точки принадлежат множеству 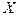 и отличны от точки
и отличны от точки 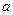 . Тогда по доказанному выше последовательность
. Тогда по доказанному выше последовательность

сходится и, следовательно, любые ее подпоследовательности имеют один и тот же предел, а это противоречит тому, что  ,
,  и
и  □
□