Краткие теоретические сведения.

При работе бруса на растяжение (сжатие) в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила 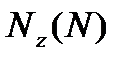, представляющая собой равнодействующую внутренних нормальных сил, возникающих в поперечном сечении бруса.

Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекции на его продольную ось всех внешних сил, приложенных по одну сторону от рассматриваемого сечения , т.е.

При растяжении продольную силу принято считать положительной ( рис а), при сжатии – отрицательной (рис. 6.1)

а) б)

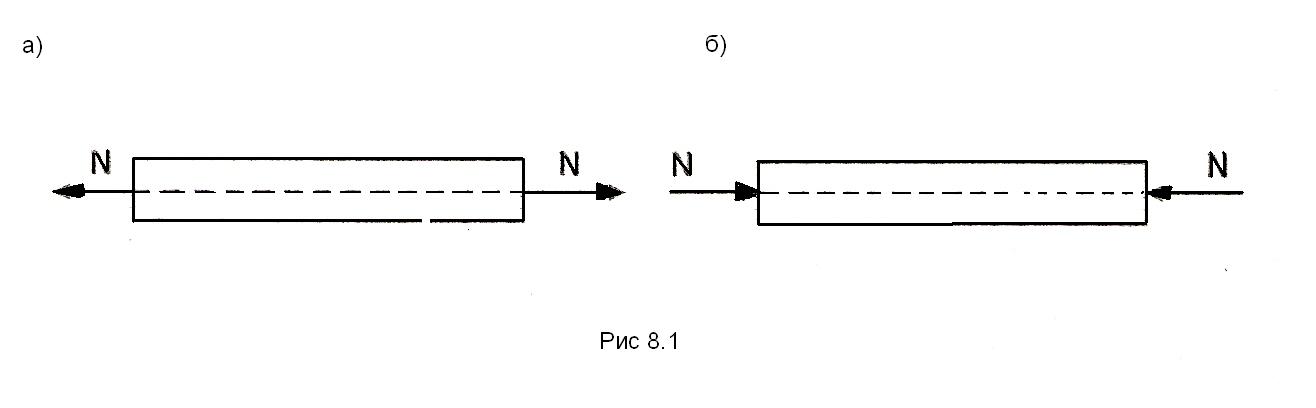
Рис. 6.1.

При растяжении (сжатии) нормальных напряжений по площади поперечного сечения распределены равномерно и вычисляются по формуле

где N – продольная сила в рассматриваемом сечении, Н; А – площадь поперечного сечения, мм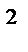

Если сечение бруса и продольная сила (или одна из этих величин) непрерывно меняются, изучение длины бруса определяют по формуле:

Изменение длины бруса (или участка бруса), имеющего постоянное поперечное сечение, определяется при условии, что продольная сила во всех поперечных сечениях одинакова по формуле:

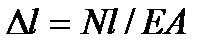
где l – длина бруса (участка бруса), мм;

А – площадь поперечного сечения бруса (участка бруса) мм ;

Е – модуль продольной упругости.

Последовательность решения задачи:

1. Уяснить условие задачи.

2. Определить значения продольных сил, применяя метод сечений.

3. Построить эпюру продольных сил.

4. Вычислить значения нормальных напряжений в сечениях.

5. Построить эпюру нормальных напряжений.

6. Используя формулу Гука, определить удлинение бруса.

7. Построить эпюру перемещений поперечных сечений на длину бруса.