Матрица коэффициентов парной корреляции
| x1 | x2 | x3 | x4 | x5 | Y | |
| x1 | 0,5662 | 0,8356 | -0,4302 | 0,9094 | -0,1501 | |
| x2 | 0,5662 | 0,1355 | 0,4683 | 0,7996 | 0,6609 | |
| x3 | 0,8356 | 0,1355 | -0,6863 | 0,5900 | -0,5123 | |
| x4 | -0,4302 | 0,4683 | -0,6863 | -0,1380 | 0,8826 | |
| x5 | 0,9094 | 0,7996 | 0,5900 | -0,1380 | 0,1019 | |
| Y | -0,1501 | 0,6609 | -0,5123 | 0,8826 | 0,1019 |
На главной диагонали данной матрицы находятся единицы, так как это коэффициенты корреляции каждого из факторных признаков с самим собой.
Рассчитаем определитель этой матрицы в Excel, воспользовавшись встроенной функцией МОПРЕД.
Легко убедиться, что определитель этой матрицы равен 0,000138, то есть очень близок к нулю. Следовательно, в данной системе факторов явно присутствует мультиколлинеарность. Поэтому все эти факторы нельзя включать в модель, а следует отобрать не более двух-трех из них.
Проанализировав коэффициенты парной корреляции, можно увидеть, что наиболее тесная связь между фактором x4 иy (то есть между доходом на 1 члена семьи и затратами на покупку непродовольственных товаров).Это вполне соответствует реальному содержательному смыслу этих показателей.
Следовательно, если включать в уравнение единственный, наиболее важный фактор, то в качестве этого фактора можно отобрать x4 , т.е.можно построить уравнение парной линейной регрессии, выражающее зависимость затрат на непродовольственные товары только от данного фактора (среднедушевого дохода семьи): y= a0 + a1 x4. Такое уравнение уже было построено.
Теперь рассмотрим, какие факторы можно включить в модель двухфакторной линейной множественной регрессии.
Коэффициенты парной корреляции между x1 и x5, а также между x1 и x3 превышают 0,8. Следовательно, эти факторы одновременно включать в модель не целесообразно.
Также очень высок (близок к 0,8) коэффициент корреляции между факторами x2 и x5. К тому же коэффициент корреляции между фактором x5 и yочень мал.
В целом, анализ матрицы коэффициентов парной корреляции показывает, что наиболее целесообразно включать в модель следующие пары факторов: x2 и x3 , либо x2 и x4. Коэффициент корреляции между ними достаточно мал, а коэффициенты корреляции между каждым из них и результативным показателем y превышает коэффициент корреляции между ними. Факторы x1 и x5 включать в модель не целесообразно, так как – несмотря на то, что между ними коэффициент корреляции очень мал (r = - 1380), но коэффициент корреляции между x5 и y еще меньше (r = 0,1019)
Перед этим мы уже убедились, что уравнение регрессии, включающее два фактора x2 и x4, дает неудовлетворительный результат. Поэтому построим уравнение y= a0 + a1 x2+ a2 x3, выражающее зависимость расходов на товары длительного пользования от числа детей (x2 ) и совокупного дохода семьи (x3).
Заполним вспомогательную таблицу для расчета параметров этого уравнения (табл.2.8).
На основе итоговых сумм, рассчитанных в нижней строке таблицы 2.8., строим систему нормальных уравнений:
 10a0+130a1+10a2=27,3
10a0+130a1+10a2=27,3
130a0+1886a1+136a2=406,3
10a0+136a1+20a2=18,3
Таблица 2.8.
Вспомогательная таблица для расчета параметров уравнения
y= a0 + a1 x2+ a2 x3
| y | x2 | x3 | x22 | x32 | x2x3 | x2y | x3y |
| 0,8 | 4,8 | 0,8 | |||||
| 0,5 | |||||||
| 2,5 | 37,5 | ||||||
| 1,5 | 4,5 | ||||||
| 27,3 | 406,3 | 18,3 |
Решаем систему нормальных уравнений методом определителей:
| Матрица А (коэффициентов) | ||
Для расчета ее определителя воспользуемся функцией МОПРЕД (которая находится среди встроенных математических функций в Excel).
Получаем Δ=19240
Заменяем последовательно каждый столбец этой матрицы столбцом свободных членов системы нормальных уравнений. Получаем еще три матрицы А0, А1, А2 и рассчитываем их определители.
| матрица А0 | ||
| 27,3 | ||
| 406,3 | ||
| 18,3 |
Определитель матрицы Ao:D0=-590,8
| матрица А1 | ||
| 27,3 | ||
| 406,3 | ||
| 18,3 |
Определитель матрицы A1:Δ1=5680
| матрица А2 | ||
| 27,3 | ||
| 406,3 | ||
| 18,3 |
Определитель матрицы A2:D2=-20724
Затем находим параметры уравнения регрессии по формулам:
a0 = D0 / Δ = -0,03
a1 = Δ1/ Δ = 0,30
a2 = D2/ Δ = -1,08
Таким образом, построенное уравнение регрессии имеет следующий вид:
y=0,03+0,30x2-1,08x3
Теперь рассчитаем для этого уравнения ошибку аппроксимации и индекс детерминации. Предварительно построим вспомогательную таблицу для расчета этих показателей (табл.2.9).
Таблица 2.9
Вспомогательная таблица для расчета ошибки аппроксимации и индекса детерминации
| Y | x2 | x3 | yx=0,03+0,30x2-1,08x3 | 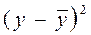
| 
| (y - yx)2 |
| 1,45 | 2,99 | 1,65 | 0,198 | |||
| 3,51 | 5,15 | 0,61 | 2,214 | |||
| 5,28 | 10,69 | 6,52 | 0,513 | |||
| 0,8 | 0,66 | 3,72 | 4,27 | 0,018 | ||
| 4,69 | 0,07 | 3,85 | 2,865 | |||
| 3,03 | 0,07 | 0,09 | 0,001 | |||
| 4,21 | 1,61 | 2,18 | 0,042 | |||
| 0,5 | 0,77 | 4,97 | 3,85 | 0,071 | ||
| 2,5 | 2,24 | 0,05 | 0,24 | 0,066 | ||
| 1,5 | 1,46 | 1,51 | 1,61 | 0,001 | ||
| 27,3 | 27,30 | 30,86 | 24,87 | 5,99 |
Как уже отмечалось, среднее значение показателя y – одинаковое для расчетных и фактических значений, так как их суммы совпадают. Поэтому в расчетах двух дисперсий вычитается одно и то же число y = 2,73 из расчетных и фактических значений признака.