Далее решаем систему методом определителей.
Вначале построим матрицу коэффициентов при неизвестных, получаем следующую матрицу А:
| матрица А | ||
| 138,6 | ||
| 1830,4 | ||
| 138,6 | 1830,4 | 1954,76 |
Находим определитель матрицы А:
Δ= 57997,84
Для расчета определителя можно воспользоваться функцией МОПРЕД (которая находится среди встроенных математических функций в Excel).
Затем подставляем в матрицу А, вместо ее первого столбца, столбец свободных членов из правой части системы нормальных уравнений.Получаем матрицу А0.
| матрица А0 | ||
| 27,3 | 138,6 | |
| 406,3 | 1830,4 | |
| 395,3 | 1830,4 | 1954,76 |
Находим определитель полученной матрицы А0
Δ0=-260310
Аналогично заменяем в матрице А поочередно второй и третий столбцы столбцом свободных членов и находим определители Δ1 и Δ2 получившихся матриц А1 и А2
| матрица А1 | ||
| 27,3 | 138,6 | |
| 406,3 | 1830,4 | |
| 138,6 | 395,3 | 1954,76 |
Δ1= 12515
| матрица А2 | ||
| 27,3 | ||
| 406,3 | ||
| 138,6 | 1830,4 | 395,3 |
D2=18466,72
Затем рассчитываем параметры уравнения регрессии по формулам:
a0 = D0 / Δ = -4,49
a1 = Δ1/ Δ = 0,22
a2 = D2/ Δ = 0,32
Окончательно уравнение регрессии имеет вид:
y=-4,49+0,22x2+0,32x4
Рассчитываем для этого уравнения ошибку аппроксимации и индекс детерминации.
Построим вспомогательную таблицу для расчета этих показателей (табл.2.5)
Таблица 2.5
| y | x2 | x4 |  = -4,49+ 0,22x2+0,32x4 = -4,49+ 0,22x2+0,32x4
| 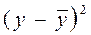
| 
| (y - 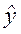 )2 )2
|
| 1,37 | 2,99 | 1,86 | 0,134 | |||
| 3,20 | 5,15 | 0,22 | 3,255 | |||
| 4,49 | 10,69 | 3,10 | 2,279 | |||
| 0,8 | -0,01 | 3,72 | 7,51 | 0,655 | ||
| 2,79 | 0,07 | 0,00 | 0,046 | |||
| 12,6 | 2,54 | 0,07 | 0,03 | 0,207 | ||
| 3,85 | 1,61 | 1,26 | 0,021 | |||
| 0,5 | 1,81 | 4,97 | 0,85 | 1,713 | ||
| 2,5 | 3,52 | 0,05 | 0,63 | 1,049 | ||
| 1,5 | 3,74 | 1,51 | 1,02 | 5,019 | ||
| 27,3 | 138,6 | 27,30 | 30,86 | 16,48 | 14,38 |
Получаем следующие результаты.
Индекс детерминации равен R2=16,48/30,86 = 0,534
Ошибка аппроксимации:

Таким образом, после включения в уравнение дополнительной переменной x2 индекс детерминации уменьшился, а ошибка аппроксимации возросла более, чем в 2 раза. Значения параметров при неизвестных существенно изменились.
Следовательно, переменная x2 в данном случае является вредной, и лучше строить уравнение парной линейной регрессии, выражающее зависимость переменной y только от одного фактора x4, чем включать два фактора x2 и x4.