Взаимное пересечение поверхностей вращения. Метод вспомогательных секущих плоскостей

Лекция №7. Пересечение поверхностей общего положения

 

Для построения линии пересечения поверхностей общего положения необходимо применение одного из методов решения позиционных задач.

Оба метода базируются на одном и том же принципе — построения линий пересечения некоторых вспомогательных поверхностей с заданными.

В качестве таковых выбираются либо плоскости (метод вспомогательных секущих плоскостей), либо сферы (метод вспомогательных секущих концентрических сфер). В любом случае задача сводится к построению линий пересечения этих вспомогательных поверхностей с заданными, а затем определению точек их пересечения между собой.

 

 

Для построения линии пересечения поверхностей вращения, расположенных произвольно в пространстве, удобно использовать известный метод вспомогательных секущих плоскостей.

Решим задачу о пересечении прямого конуса и сферы (рис. 7.1).

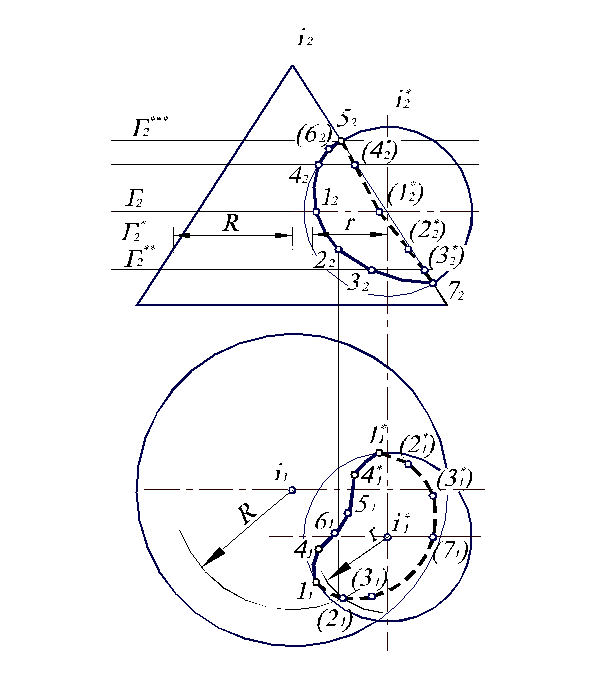
Рис. 7.1. Пересечение конуса и сферы.

 

Ось конуса – горизонтально-проецирующая прямая i , а ось сферы - i*.

В качестве вспомогательных секущих плоскостей выбираем горизонтальные плоскости уровня, так как на П₂ линиями их пересечения с конусом и сферой являются горизонтальные прямые, а на П₁ – дуги окружностей, построение которых не вызывает затруднений. Так, для произвольной горизонтальной плоскости Г* имеем: линиями ее пересечения с конусом и сферой являются окружности, которые на П₂ проецируются в горизонтальные прямые, совпадающие с Г₂*. Тогда на П₁ эти линии представляют собой дуги окружностей, радиусами R и r, каждый из которых равен расстоянию от соответствующей оси до контура конуса и сферы на П₂. Пересечение этих дуг и дает точки 2₁ и 2₁*, являющиеся искомыми горизонтальными проекциями точек пересечения конуса и сферы. Проводя вертикальную линию связи до пересечения с Г₂*, получаем фронтальные проекции 2₂ и 2₂* найденных точек.

Аналогично находим горизонтальные и фронтальные проекции точек 1, 3, 4, 1*, 3*, 4*, которые являются парными, так как лежат в одной горизонтальной плоскости уровня. Исключение составляет точка 5, поскольку она является точкой перегиба линии пересечения.

Характерными в данном примере будут точки 1 и 1*, лежащие на экваторе сферы. Как видим, эти точки определяют на П₁ переход видимого участка искомой линии в невидимый. Также характерными являются точки 6 и 7, лежащие на главном меридиане, которые на П₂ разделяют видимый и невидимый участки линии пересечения конуса и сферы.

Проведя плавные кривые через найденные проекции точек, получим фронтальную и горизонтальную проекции линии пересечения конуса и сферы.