Введение: угрозы существованию и эффекты наблюдательной селекции

Человечество стоит перед рядом глобальных угроз, расположенных как в близком, так и далёком будущем. Для любого человека, заинтересованного в будущем нашего биологического вида, эти угрозы представляют теоретический интерес; они также напрямую связаны с принимаемыми сейчас прикладными и стратегическими решениями. Общее понимание возможных глобальных катастроф возросло благодаря последним открытиям в геохимии, эволюции человека, астрофизики и молекулярной биологии [1-6]. Это исследование рассматривает подмножество катастроф, называемых угрозами существованию (existential risks -УС), которые могут привести либо к уничтожению разумной жизни на Земле, либо навсегда и значительно ограничат её потенциал [7]. В качестве примеров УС можно взять тотальную ядерную войну, столкновении 10-км (или большего) астероида или кометы с Землёй, международное или случайное злоупотребление био- или нано технологий, или неограниченно растущее глобальное потепление.

Существует множество таксономий УС [7]. Таксономия, основанная на причинных факторах, нам подходит больше всего. Мы различаем: (1) естественные УС (столкновения с астероидами и кометами, супервулканизм, неантропогенные изменения климата, взрывы сверхновых звёзд, гамма-всплески, случайный фазовый переход вакуума); (2) антропогенные УС (ядерная война, биологические катастрофы, искусственный интеллект, нанотехнологические риски); (3) промежуточные УС, вызываемые взаимодействием человечества и природы (новые болезни, неограниченно растущее глобальное потепление). Далее, мы в основном рассматриваем естественные УС [8].

Целью данной статьи является исследование эффектов наблюдательной селекции, влияющих на оценку вероятности некоторых УС и способных привнести антропное искажение в анализ рисков[136]. Антропное искажение может быть объяснена через форму искажение в выборке примеров, при которой выбирается подмножество примеров, локально связанных с наблюдателем, вместо множества событий, полностью охватывающего предметную область. Мы показываем, что эффект наблюдательной селекции делает ненадёжными оценки вероятности некоторых прошлых УС. Мы утверждаем, что антропное искажение может привести к недооценке вероятностей ряда глобальных катастроф.

Мы расписываем простую «карманную» модель этих эффектов во второй части статьи, тогда как её обобщение находится в третьей части. Аргументация развивается в четвёртой части, а в пятой мы рассматриваем актуальность антропного искажения для ряда УС. В последней, шестой части мы рассматриваем вопросы применения теории эффектов наблюдательной селекции к глобальным катастрофам.

«Карманная» модель антропного искажения[137]

Основой нашего подхода является Байесова формула расчета условной вероятности:

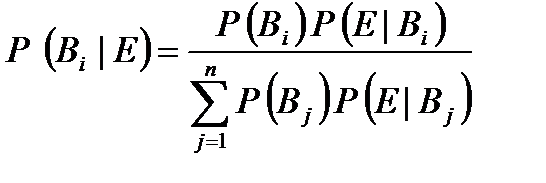, (1)

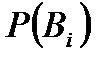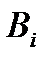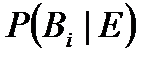где является априорной вероятностью истинности гипотезы , и – условной вероятностью истинности гипотезы 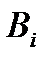при свидетельстве . В качестве свидетельства мы будем рассматривать сам факт нашего существования. Факт нашего существования требует для себя множество биологических, химических и физических предпосылок. В частности, наше существование подразумевает, что цепочка земной эволюции не была прервана глобальной катастрофой. С этим условием связаны некоторые неопределённости, часть из которых мы должны обсудить далее. Гипотезы B1, B2, …, Bn обозначают произошедшие или не произошедшие катастрофы определённого типа, случившиеся за определённый промежуток времени; примерами подобных гипотез являются: «Произошло не менее пяти случаев столкновений Земли с астероидами или кометами величиной от 10 до 20 км за последние 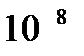лет», или: «За промежуток от 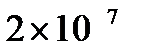до 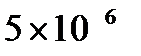до настоящего момента и не ближе чем 10 парсек до Солнца, не происходило ни одного взрыва сверхновой звезды».

Рассмотрим простейший пример: исключительно разрушительную и единичную глобальную катастрофу, – под эти условия подходит извержение супервулкана Тоба [9]. Свидетельство, которое мы хотим учесть с помощью Байесового подхода, – это факт нашего существования в настоящую эпоху. На Рис. 1 мы схематично отобразили эту ситуацию: P – априорная вероятность некой глобальной катастрофы, Q – вероятность выживания человечества после этой катастрофы. Мы должны предположить, что эти две вероятности: (1) являются константами, (2) должным образом нормализованы и (3) относятся к определённому интервалу в прошлом. Событие 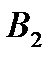обозначает , что катастрофа происходит, а событие 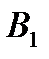– что катастрофа не происходит, под E мы обозначаем информацию о нашем собственном существовании.

время

Рис. 1. Схематичное изображение нашей карманной модели единичного катастрофического события. P – это априорная вероятность глобальной катастрофы, Q – вероятность выживания человечества, E – факт нашего существования в настоящий момент.

Для этого примера Байесова формула принимает вид:

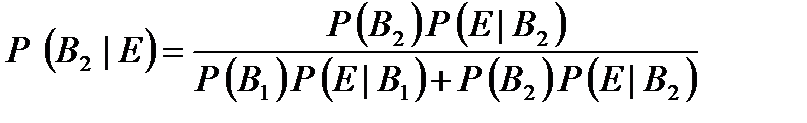, (2)

Что даёт значение постериорной вероятности:

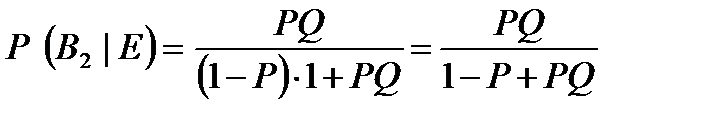. (3)

Мы можем определить коэффициент самоуверенности:

, (4)
   

что в данном случае приводит к:

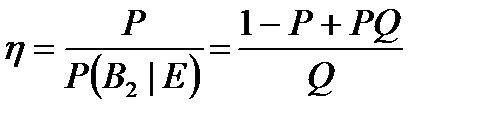. (5)
   

Чем больше становится η (начиная с единицы), тем наши умозаключения о прошлом становятся всё более ненадежными, и мы недооцениваем вероятность будущих катастроф. Например, возьмём Q=0.1 и P=0.5 (или произойдёт, или не произойдёт с равной вероятностью), для событий, сравнимых по размеру с извержением Тоба; также примем, что во время человеческой эволюции эти события случаются один раз в миллион 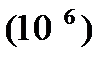лет 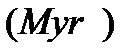с вероятностью выживания человечества при каждом из них равной 0.1. С этими условиями коэффициент самоуверенности 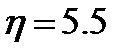, что означает – реальная вероятность превышает нашу первоначальную оценку в 5.5 раз. Значения коэффициента самоуверенности, в виде функции тяжести последствий (при вероятности вымирания 1–Q), показаны на Рис. 2.

Также учтите,

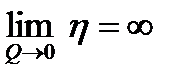. (6)

вероятность вымирания

Рис. 2. Коэффициент самоуверенности в качестве функции от вероятности вымирания 1–Q в нашей карманной модели единичного события. К различным значениям вероятности P применено цветовое кодирование (цвета различимы в электронной версии). Мы заметили, что искажение от самоуверенности выше всего для маловероятных событий.

Коэффициент самоуверенности становится очень большим для чрезвычайно разрушительных событий. В результате, мы не должны быть уверены в исторических оценках вероятности событий, приводящих к безусловному вымиранию человечества (Q=0). Пусть этот вывод и выглядит очевидным, широкого признания он не получил. Например, широко известная аргументация Хата и Риса (Hut and Rees), работающих с гипотетическим риском квантовой неустойчивости вакуума в экспериментах физики высоких энергий, не учитывает влияния антропного искажения, из-за чего частично вводит в заблуждение [10].

Эти рассуждения также применимы к исключительно редким, но, тем не менее, возможным событиям, примером которых являются странные астрономические инциденты, способные сорвать Землю с орбиты и превратить в межзвёздную планету (см. Лаглин и Адамс (Laughlin and Adams), оценивающих вероятность подобного события на оставшееся время существования Солнечной системы [11]). Выводы о чрезвычайной малой вероятности прохождения Солнечной системы неподалёку от другой звёздной системы, нейтронной звезды или чёрной дыры, а значит и чрезвычайно малых рисков этого события, не могут быть получены только из прошлого нашей планетарной системы. Принятие дополнительной информации, основанной на понимании окружения Солнечной системы в пространстве Млечного Пути и характеристиках масс звёздных объектов, позволяет нам заключить, что по отношению к этим рискам мы находимся в безопасности, а не непредвзяты и убедительны. С другой стороны, не для всех возможных угроз собрано достаточное количество дополнительной информации.