Основные понятия математической логики

Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать, истинно оно или ложно. Например:

«Лед — твердое состояние воды» — истинное высказывание.

«Треугольник, это геометрическая фигура» — истинное выска­зывание.

«Париж — столица Китая» — ложное высказывание.

6 < 5 — ложное высказывание.

Логические величины:понятия, выражаемые словами: ИСТИ­НА, ЛОЖЬ (true, false). Следовательно, истинность высказываний выражается через логические величины.

Логическая константа:ИСТИНА или ЛОЖЬ.

Логическая переменная:символически обозначенная логическая величина. Следовательно, если известно, что А, В, X, Y и пр. — переменные логические величины, то это значит, что они могут принимать значения только ИСТИНА или ЛОЖЬ.

Логическое выражение— простое или сложное высказывание. Сложное высказывание строится из простых с помощью логичес­ких операций (связок).

Логические операции.В математической логике определены пять основных логических операций: конъюнкция, дизъюнкция, от­рицание, импликация, эквивалентность. Первые три из них со­ставляют полную систему операций, вследствие чего остальные операции могут быть выражены через них (нормализованы). В ин­форматике обычно используются эти три операции.

Конъюнкция(логическое умножение). В русском языке она выражается союзом И. В математической логике используются знаки & или 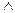. Конъюнкция — двухместная операция; записывается в виде: А 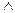В. Значение такого выражения будет ЛОЖЬ, если значе­ние хотя бы одного из операндов ложно.

Дизъюнкция (логическое сложение). В русском языке этой связ­ке соответствуют союз ИЛИ. В математической логике она обозна­чается знаком v. Дизъюнкция — двухместная операция; записыва­ется в виде: A v В. Значение такого выражения будет ИСТИНА если значение хотя бы одного из операндов истинно.

Отрицание.В русском языке этой связке соответствует частица НЕ (в некоторых высказываниях применяется оборот «неверно что...»). Отрицание — унарная (одноместная) операция; записы­вается в виде: 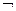А или .

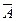Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИ­НА или ЛОЖЬ.

Пример 1. Рассмотрим сложное высказывание: «Число 6 делит­ся на 2, и число 6 делится на 3». Представить данное высказывание в виде логической формулы. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Toгда соответствующая логическая формула имеет вид: А & В. Очевидно, ее значение — ИСТИНА. Пример 2. Рассмотрим сложное высказывание: «Летом я поеду в деревню или в туристическую поездку».

Обозначим через А простое высказывание «летом я поеду Я деревню», а через В — простое высказывание «летом я поеду в туристическую поездку». Тогда логическая форма сложного высказывания имеет вид

A В.

Пример 3. Рассмотрим высказывание: «Неверно, что 4 делится на 3».

Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид 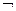А

Правила выполнения логических операций отражены в следующей таблице, которая называется таблицей истинности.

Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицания, конъюнкция, дизъюнкция. Кроме того, на порядок операции влия­ют скобки, которые можно использовать в логических формулах.

Приложения математической логики в базовом курсе

Математическая логика в базах данных. При изучении базового курса информатики ученики впервые встречаются с элементами математической логики в теме «Базы данных» (БД). В реляцион­ных БД логическими величинами являются поля логического типа. Логический тип используется наряду с другими типами полей, и ученики должны научиться выделять его.

Первое понятие о логической величине можно дать как ответ на альтернативный вопрос. Например: «Имеется ли данная книга в библиотеке?» или «Поступил ли абитуриент в университет», или «На улице идет дождь?» и т.п. Ответами на такие вопросы могут быть только «да» или «нет». Синонимами являются «истина», «ложь»; «true», «false». Если поле таблицы будет принимать только такие значения, то ему назначается логический тип.

Например, реляционная база данных ФАКУЛЬТАТИВЫ со­держит сведения о посещении учениками трех факультативов по геологии, цветоводству и танцам. На реляционном языке ее струк­тура описывается так:

ФАКУЛЬТАТИВЫ (УЧЕНИК. ГЕОЛОГИЯ, ЦВЕТОВОДСТВО, ТАНЦЫ)

Поля ГЕОЛОГИЯ, ЦВЕТОВОДСТВО и ТАНЦЫ будут иметь логический тип. Значение ИСТИНА для каждого поля обозначает, что ученик посещает данный факультатив, а ЛОЖЬ — не посещает.

 

Логические выражения используются в запросах к базе данных в качестве условий поиска. Логические выражения разделяются на простые и сложные. В простых выражениях всегда используется лишь одно поле табли­цы, и не применяются логические операции. В сложных логичес­ких выражениях используются логические операции. Простое логическое выражение представляет собой либо имя поля логичес­кого типа, либо отношение (в математике говорят «неравенство»). Отношения для числовых величин сохраняют смысл математи­ческих неравенств; при вычислении отношений для символьных величин учитывается лексикографический порядок; даты сравни­ваются в порядке их календарной последовательности.

Основная проблема — научить учеников формальному представлению условий поиска в виде логических выражений. На­пример, от фразы «найти все книги, лежащие выше пятой полки» нужно перейти к логическому выражению: ПОЛКА > 5; или условие «выбрать всех неуспевающих по физике» представить в виде: ФИЗИКА < 3; или «выбрать все дни, когда шел дождь» ОСАДКИ = «дождь».

Особое внимание надо обратить на использование полей логического типа в условиях поиска. Обычно к ним не применяются отношения. Логическое поле само несет логическое значение: «истина» или «ложь». Например, условие «выбрать всех учеников, посещающих танцы» представится одним именем логического поля ТАНЦЫ.

Сложные логические выражения содержат в себе логические операции. Рассматриваются три основные операции математической логики: конъюнкция (И), дизъюнкция (ИЛИ), отрицание (НЕ).

Обычно при объяснении этого вопроса учитель отталкивается от семантического смысла высказываний на русском языке, содержащих союзы И, ИЛИ, частицу НЕ. Например, высказывание: «Сегодня будет контрольная по алгебре И по физике» справедливо, если состоятся обе контрольные и ложно, если хотя бы одна не состоится. Другое высказывание: «Сегодня будет контрольная по алгебре ИЛИ по физике» будет истинным, если со­стоится хотя бы одна контрольная работа. И, наконец, высказы­вание: «Сегодня НЕ будет контрольной» истинно, если конт­рольная не состоится, т. е. если высказывание о том, что сегодня будет контрольная, оказывается ложным. Из подобных примеров учитель делает выводы о правилах выполнения логических опера­ций: если А и В — логические величины, то выражение

• А и В истинно только в том случае, если истинны оба операнда;

• А или В ложно только в том случае, если ложны оба операнда;

• не А меняет значение логической величины на противопо­ложное: не истина — ложь; не ложь — истина.