Принципы построения ДМ

Эндо- и экзогенные переменные

Половой деморфизм продолж-ти жизни

2 прогноза:

1. величина фоновой компоненты практически одинакова для м. и ж. Различие в продолж-ти жизни м. и ж. явл. устойчив. и м. меняться лишь в том же направлении, что и сама продолж-ть жизни.

2. ООН: возмож-ть реал. уменьшения полов. различий в продолж-ти жизни.

 

МОДЕЛИРОВАНИЕ ДЕМОГР. ПРОЦЕССОВ

Демогр. модели (ДМ) предназначены для описания, как правило, с помощью матем. методов состояния н-я и его изменений, отдел. элементов воспр-ва н-я или процесса этого воспр-ва в целом. Термин ДМ начал широка примен-ся в науч. лит-ре с 40х г. 20в. Большинство моделей не претендует на описание моделируемого процесса во всем многообразии его особенностей. Так многие модели учитывают лишь некот. соц.-экон. и демогр. хар-ки. Так большая гр. наиб. распростр. моделей (моделей воспр-ва н-я) рассм-ют диффернциацию н-я лишь по полу и возрасту. При построении и use ДМ приходится абстрагироваться отцелого ряда характерных признаков и св-в омоделирования, кот. либо явл. несущественными либо расм-ся на несуществ. с т.зр. иссл-ля, т.е. в основе моделирования лежит формализация ???Ота?? моделирования.

Кажд. модель хар-ся набором эндогенных и экзогенных переменных модели и системой соотн-й м/д этими переменными.

Эндогенные переменные лпред-ся в самой ДМ (пр. числ-ть н-я, число демогр. событий, их интенсивность, динамика и т.д.)

Экзогенные переменные опред-ся ане модели, по своему хар-ру м.б. как демогр. так и недемогр. (биолог., эконом., соц.-психол. и др.)

В число экзогенных переменных обязательно входит:

- календар. время

- длит-ть пребывания в дан. демогр. состоянии (возраст)

Эндогенные переменные расм-ся как ф-ции длительности состояния или возраста (демометрич. ф-ции не имеют аналит. выражения (т.е. формулу) и задаются с помощью таблицы или графика).

Наряду с чисто ДМ с 70х г. 20в. большое распр-ние получили демогр.-эконом. модели с эконом. эндогенными переменными, устан-щие взаимосвязь роста н-я и эконом. развития. В зависимости от типа модели система соотнош-ний м/д ее переменными м. задаваться в виде матем. формул, уравнений и их систем, числов. таблиц, опред. правил.

1. правила опред-ния экзогенных переменных модели (на основе данных статистики н-я и др. инф-ции)

2. правила интерпритации эндогенных переменных модели (т.е. толкование их значений как хар-к реально протекающих демогр. процессов)

3. ограничения, опред-щие область применения модели

4. гипотезы, положен. в основу модели. Гипотеза – это предположение о св-вах и особенностях Ота моделирования, вытекающее из конкр. демогр. ан-за

5. соглашение, принимаемое при ее построении. Соглашение – это условн. допущения, кот. привносятся в модель с целью упростить ее матем. аппарат и рассчеты, и т.д.

ДМ возникает как абстрактная матем. модель, кот. м.б. отнесена к любому из н-й, удовлет-щих принятым ограничениям. Придав переменным конкр. кач. и колич. значения получают модель конкр. н-я.

ВИДЫ ДМ

а) - макромодели – описывают демогр. процессы на уровне всего н-я или отдел. его частей.

- микромодели описывают демогр. процессы на уровне индивида или семьи через последовательность демогр. событий в жизни демогр. единиц

б) - стохастические (вероятност.) use матем. вероят-ть. Сложность их постоения: большинство демогр. сов-тей не однородны в статистич. смысле. Все микромодели явл. стохастичными.

- детерминистские – традиционны для Д. При таком подходе при построении модели use не матем., а демогр. вероят-ть. Ими явл. все макромодели.

в) - модели в кот. время и возраст входят как непрерывные переменные наз. непрерывные

- содели в кот. они приняты изменяющимися с опред. шагом наз. дискретными (микромодели.

Среди макромоделей одинаково распр-ны и непрерывные и дискретные.

ПРИМЕНЕНИЕ ДМ В СОВР. Д.

1. для получения колич. хар-к демогр. процессов и явл-й. Многие распрстр. демогр. К. рассчит-ся только на моделях (ср. предстоящ. продол-ть жизни, нетто-к. воспр-ва).

2. основа для демогр. прогноза.

3. use при текущих и ретроспект. демогр. рассчетах, особенно когда статистич. данные отсутствуют или мало достоверны.

4. в значит. степени опред-ют хар-р сбора и обработки инф-ции о н-и.

5. представляют собой область для разного рода демогр. экспериментов (мыслен.) в частности для оценки эфф-ти мер дамогр. политики. Применяются практически во всех разделах Д.

СТАЦИОНАРНОЕ Н-Е

Исходное положение модели стационар. н-е

1) неизменный порядок вмирания, опис. сов-тью показателей таблицы дожития

2) постоянство ежегод. чисел рожд-ний (точнее постоянство плотности рождений)

3) отсутствие миграции (закрытое н-е).

Пусть постоян. годовое число рожд-й равно N. Рассм-м табл. дожития, в кот. исходн. число l₀=1 (число новорожд. =1). _ все послед. l_x также выражаются в долях единицы (доли доживающих до возраста х из первоначального поколения). (Пр. l₁₀ в этом случае математически равно вероят-ти для новорожденного достичь возраста 10 лет.) Число живущих в возр. 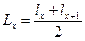доля живущих в возр. х из первонач. поколения. _ Если N – число родившихся за год, то из них девочек ΘN [тета], а мальчиков (1- Θ)N, где Θ – доля девочек; (1-Θ) – доля мальчиков.

ЗАМЕЧАНИЕ: Θ обычно = 0,488

Тогда в каждый дан. момент времени в таком н-и будет в любом возрасте х (не обязательно точно)

ΘNL_x^ж – число жен.; L_x^ж – число живущих жен. возраста х в долях единицы

(1-Θ)NL_x^м – число мужчин; L_x^м – число живущих муж. в возр. х в долях единицы

Числа Lx наз. числами "живущих в стационарном н-и".

Т.к. а) N=const и исходн. число при рождении для всех возрастов одинково

б) L_x^ж , L_x^м , Θ – не зависят от времени

То найденное число муж. и жен. в возрасте х – остается также const

_Важнейш. св-во стационар. н-я!!! – числ-ть всех его половозр. групп, а следовательно и общ. числ-ть и половозр. стр-ра стацион. н-я остается постоянными, т.е. не меняется во времени.

Общ. числ-ть лиц обоего пола в кажд. возр. будет NL_x, где L_x – число живущих в возрасте х в долях единицы

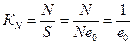Числ-ть всего н-я , где е₀ – ср. продол-ть предстоящ. жизни при рождении из таблицы дожития _К. рожд-ти стацион. н-я . Т.к. числ-ть стацион. н-я не меняется, то Δе=0_КΔе=0_

(Пр. е₀=60 лет, то в стац. н-и ежегодно сменяется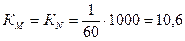‰=1,06 % н-я)

Пример: _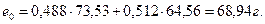Такое стацион. н-е хар-ся след. рожд-ю и смерт-ю ‰

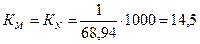Зная число рожд-й в год м. получить общ. числ-ть н-я и число м. и ж.

Пусть N=1 млн. чел., тогда число муж. Sм=0,512∙64,56∙1000000=33054720 чел; а Sж=0,488∙73,53∙1000000=35882640 чел. (т.к. при l₀=1, сумма 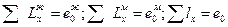_число мужчин всех возрастов равно

Данная модель находит применение:

1. в палеодемогр. исл-ниях для уточнения параметров воспр-ва в первобытное время
2. при ан-зе соврм. н-я в отдел. странах, где имеется довольно высокие показатели N и М, но примерно равные.

Модель стацион. н-я явл. результатом действия табл. дожития на неизмен. число ежегод рождений.

Модель стабильного н-я – результат действия табл. жожития на чило ежегод. рождений, кот. меняются из года в год в соответствии с постоян. К.

Исходные положения:

1) постоян. порядок вымирания

2) изменение чисел рождения в геометр. прогрессии

3) отсутствие внеш. миграции

! Условия 1 и 3 не отлич. от условий модели стационар. н-я.

Обозначим знаменатель прогрессии, в кот. изменится годов. число рождений, е^к . Пусть в год, принятый за нач. отсчета, родилось N₀ чел., тогда в след. год родится N₀·e^к чел. Еще через год N₀e^2к чел. и т.д. А в годы предшеств. отсчету N₀e^-к, N₀^-2к и т.д. В общ. случае в год t относительно начала отсчета числа рождений = N₀e^кt.

Проведя рассуждение аналогичное модели стацион. н-я получим, что в общ. случае в возр. х через t лет после начала отсчета в стабильн. н-и будет и

В этих числах м. выделить общ. множитель, зависящий от времени _ числ-ти всех половозр. групп меняется в геометр. прогрессии с одним и тем же знаменателем _соотн-е числ-ти половозр. групп не меняется _половозр. стр-ра группы не меняется (доля гр. н-я остается неизмен. в общ. числ-ти н-я).

Общ. числ-ть н-я в возрасте х

Общ. числ-ть н-я всех возрастов

В этой формуле от вр. t зависит только множитель e^kt он меняется в геометр. прогрессии со знаменателем е^к (тем же, что и в числе рождений) _Числ-ть стабил. н-я и его половозр. групп меняется в геометр. прогрессии с тем же знаменателем, что и число рождений. Это означает что соотн-е м/д числом рождений и числ-тью н-я остается неизмен. " значит в стабил. н-и рождаемость не меняется (в 1 год исчисл-ся к=0; е^кt=1)

ЗАМЕЧАНИЕ: доказано, что при изменении числ-ти н-я в геометр. прогрессии _

Если k>0, то е^-кх с #х уменьшится _ число рождений (и н-я) # (растущее стабил. н-е)

Если k<0, то е^-кх с #х возрастает _ число рождений (и н-я) $ (убвающее стабил. н-е)

Если k=0, то получаем частный случай стабил. н-я – стационар. н-е, т.е. стабил. н-е тем "моложе", чем выше К. естеств. прироста

Примеры стабил. н-я с разн. возр. стр-рой

 

 

Стабил. н-е бывает разл.

Св-во эргодичности состоит в том, что влияние прошл. возр. стр-ры н-я на послед. со врем. постепенно ослабевает и возр. стр-ра становится зависящей от режима воспр-ва в предшеств. период. Различают св-ва сильной и слабой эргодичности:

1) Сильная эргодичность. Если интенсивность рожд-ти и смерт-ти к.-л. н-я становится неизменной во вр., то возр. стр-ра такого н-я и все ее параметры какими бы они не были до этого постепенно приближается к некот. передельн. значениям однозначно зависящим от возр. интенсивности рожд-ти и смерт-ти. В этом случае н-е наз. АССИМПОТИЧЕСКИ СТАБИЛЬНЫМ, а процесс приближения возр. группы к предел. значениям – СТАБИЛИЗАЦИЕЙ н-я. Этот процесс заключается в том, что при сохранении впредь неизменного существующего режима воспр-ва н-я обнаружит тенденцию превращающего в стабильное, отвечающее этому режиму. Это св-во use в прогнозах на 50-100 лет вперед. На основе модели стабил. н-я м. рассчитать бесконеч. множество видов стабил. н-я со своими параметрами.

Св-во сильн. эргодичности открыл в 20в. амер. демограф Дж. Лотка.

2) Св-во слабой эргодичности не предполагает неизменность возр. интенсивностей рожд-ти и смерт-ти и допускает изменение возр. стр-ры во вр. Если 2 н-я, начиная с некот. момента вр., обладают одинак. возр. интенсивн-ми рожд-ти и смерт-ти (м.б. изменяющимися во вр.), то они постепенно приобретают одинак. возр. стр-ру.

Истин. К. естеств. прироста (К. Лотки)

Представляет собой К. естеств. прироста стаб. н-я, кот. получается из дан. н-я при дан. режиме воспр-ва в результате процесса стабилизации , где Rn – нетто-коэф. воспр-ва н-я;

Т – длина поколения, интервал м/д сред. возр. родителей и годом рожд-я сред. ребенка.

Для жен. это ≈30±2 года; для муж. чуть больше

Если Rn>1, то k>0 (расшир. воспр-во)

Rn=1, то k=0 (простое воспр-во)

Rn<1, то k<0 (суженное воспр-во)

 

ДЕМОГР. ПРОГНОЗИРОВАНИЕ (ДП)

(пробел)

2. Точечн. прогнозы (прогнозируемая величина м.б. задана 1 числом – точечный прогноз, интервалом – интервальный).

3. Условн. и безусловн. прогнозы. Условн. – прогноз, кот. состовляется в завис-ти от наступления (ненаступления) к.-л. события. Безуслов. прогноз таким свойством не хар-ся.

4. Единич. и множеств. прогнозы (в завис-ти от кол-ва объектов прогнозирования)

а) аналичтич. – для ан-за влияния изменений в демогр. процессах на стр-ру н-я

б) прогнозы предостережения предназначены для демонтрации перпектив, кот. следует избегать

в) норматив. прогнозы содержат опред. рекомендации, конкрет. условия достижения тех или иных результатов (Пр. в обл. демогр. политики)

5. По хар-ру применяемых методик рссчета:

а) прогнозы общ. числ-ти н-я

Известно, что демогр. процессы обладают инерционностью, т.е. св-вом достаточно длител. время сохранять осн. черты и параметры своего развития, поэтому при ДП общ. числ-ти н-я исл-ся методы учитывающие вероят-ть сохранения осн. черт и параметров воспр-ва н-я на будущее (методы экстраполяции).

Метод экстрополяции основан на ан-зе опред. исходн. данных и принятии через относительно хар-ра буд. изменений изучаемого явл-я или процесса. Принятым прогнозам д. соответ-ть выбран. для экстраполяции аналитич. ф-ция. Простейшая – линейная ф-ция. Она применяется при допущении условий постоян., абсол. прироста н-я и ее уравнение имеет вид: . При условии пост. К. Δо применяется экспоненциальная ф-ция , где к – коэф. Δо в долях единицы. В кач-ве аналит. ф-ций выбираются и др. ф-ции. Выбор подходящей ф-ции (кривой) – самый сложн. этап в прогнозе.

При use метода экстрополяции нужно следить, чтобы период, выбран. для ДП, был однородный и относился к одному этапу истор. развития.

ДП общ. числ-ти н-я делается также с помощью регрессион. моделей. Он основан на построении многомерн. моделей, учитывающ. некот. число факторов, влияющих на динамику общ. числ-ти н-я или отдел. его групп. При этом все факторы расм-ся как независ. переменная, а рассчитыв. числ-ть как завис. переменная. Регрес. модели как метод ДП основаны как правило на предположении опред. степени завис-ти динамики н-я и соц.-экон. факторов. Этот вид прогнозов часто наз. эконом. видами ДП. !!! – регрес. модели очень упрощают причин.-следств. связь.

б) прогнозы числ-ти и стр-ры н-я

Осн. метод с помощью кот. производится перспектив. расчет стр-ры н-я – метод передвижки возрастов. База этого метода – данные о половозр. составе н-я по послед. переписи и показатель таблиц дожития (К. дожития (передвижки)). К. дожития

Возраст х или х+4	Числ-ть н-я по возр. и полу (перепись, Sx	Рх, К. дожития из табл. дожития расчит. за год переписи	Числ-ть н-я к след. шагу перспектив. расчета, Sx

 

ТОЧНОСТЬ ДП

Проблема точности и достоверности ДП самое слабое их место. Прогноз выполненый в рамках 5% уровня точности м. считать удачным. Уровень точности данных периписи н-я 1-2%.

Осн. причины возм. ошибок и неточностей явл.:

1) неправ. выбор гипотез относительно осн. составляющих ДП

2) неправ. выбор методов и методик вычисления

3) период вр. на кот. делается расчет. Если прогноз расчитан на срок более 10 лет, то его точность м.б. достаточно высока. При # прогноз. периода до 25-30 лет – точность ДП $. Это связано с тем, что длина поколения оставляет ≈30 лет.

4) этап демогр. перехода на кот. находится н-е дан. территории. Прогнозировать демогр. процессы для н-я на начал. стадиях демогр. перехода значит-но труднее, чем для н-я наход-ся на последних стадиях демогр. перехода.

5) стихийн., соц., эконом. катаклизмы, кот. м. сделать прогноз полностью непригодным.

Самый верный критерий точности прог-за н-я явл. совпадение прогноз. и фактич. данных. Но такое сравнение возможно либо по истечении срока прог-за либо при ретроспективном ДП.

Для выбора наиб. точного метода ДП первоначально прогноз проводится на ретроспектив. данных на текущий период. При этом для оценки точности ДП use след. величины:

1. сред. квадратич. ошибка прогноза , где Sn – прогнозир. числ-ть;

Sф – фактич. числ-ть

n – число поколений

Чем <σ, тем лучше прогноз

2. К. несоответствия

Если V=0, то полное совпадение фактич. и прогнозир. данных

Если V>1, то прогноз дает худшие результаты чем предположения о неизменности дан. явл-я.

Компьют. обеспечение ДП

Служат для описание демогр. ситуации

(нет больше)

 

ДЕМОГР. СИТУАЦИЯ (ДС)

Это состояние демогр. процессов, состава и размещения н-я в опред. вр. (чаще в опред. году). Обычно расм-ся в целом по стране или отдел. ее частям.

При оценке ДС учитываются границы колебания важнейш. демогр. К.

Общ. К. рожд-ти: 0‰ – маловероятно

50-50‰ – макс. среднегод. значение в наиб. благоприят. для рожд-ти ситуации (молод. н-е)

14-16‰ – сознат. ограничение рожд-ти осн. массой н-я

Общ. К. смерт-ти: 0‰ – маловероятно для больших групп н-я

4-5‰ – наиб. благоприят. условия для минимализации смерт-ти (рубеж реальности м)

≈50‰ – макс. величина, но при отсутствии масс. эпидемий и войн.

Суммар. К. (воспр-ва н-я): 10-12 детей при наиб. репродуктивности у жен. При отсутствии массов. сознат. ограничения рожд-ти >4

Брутто-коэф. воспр-ва: 5,9 – макс. величина (с учетом доли жен. в н-и)

>2 – при отсутствии массов. сознат. ограничения рожд-ти

Нетто-коэф. воспр-ва (всегда <брутто-коэф.). Разница зависит от уровня смерт-ти женщин репродуктив. возраста. В совр. условиях этот уровень незначителен _ К. отличаются лишь на сотые, тысячные. Пределы вариации нетто-коэф. ≈совпадают с границами брутто-коэф. в запад. странах.

Сред. продол-ть пердстоящей жизни: 84 лет – макс. (Япония) 25 лет – миним. (Афганистан, Африка)

 

ОПТИМУМ Н-Я

это наиб. рациональный из всех возможных с т.зр. избранного критерия (их системы) тип воспр-ва н-я. Различают:

1. динамический оптимум – желательная интенси-ть демогр. процессов и развития демогр. стр-р
2. статический оптимум – состояние на опред. дату.

Впервые понятие оптимума ввел шведск. экономист Викселль в 1910г.

 

ДЕМОГР. ПЕРЕХОД

Это концепции, применяемые в совр. Д. для объяснения истор. типов воспр-ва н-я. Термин был предложен в 1945 г. амер. демогр. Ноутстайнем. Разработка 1-ой концепции демогр. перехода осущ-на с 1909по1934г. фр. Ландри.

К концу 19в. было установлено, что уровни рожд-ти и смерт-ти обуслов-ся не биолог. законами, а соц. условиями (в осн.). Причем в процессе истор. развития происходит глубок. качеств. изменения типов воспр-ва н-я.

Общ. элемент концепций демогр. перехода – периодизация демогр. развития. Выделяются 3 типа воспр-ва н-я:

1) архетип. Относится к ран. этапу чел. истории, к доклассовому об-ву. Он изучен слабо, его существование – гипотеза.

2) традицион. (экстенсивный). Характерен для докапиталист. классов. аграрн. об-в и на ранних стадиях развития капитализма.

Осн. черты: 1) высок. смерт-ть; 2) низк. уровень развития производ. сил; 3) больш. завис-ть чел-ка от стихийн. сил природы; 4) неустойчивость воспр-ва н-я; 5) низк. экономичность. Для архетипа и традицион. типа темп прироста н-я в осн. опред-ся уровнем смерт-ти, кот. достаточно велик, а рожд-ть высока для компенсации высок. уровня смерт-ти.

3) современ. (интенсивный).

Совр. тип возникает в экономике развитых стран (капитал.). Вызывается скачком в развитии производ. сил, переходом от аграр. к индустр. экономике, и как следствие уменьшение зависимости чел-ка от природы.

Осн. черты: 1) снижение смерт-ти; 2) снижение рожд-ти; 3) повышение гибкости демогр. отн-й; 4) повышение экономичности и устой-ти процесса воспр-ва. Для совр. типа воспр-ва н-я и переходных к нему типов естеств. прирост опред-ся уровнем рожд-ти, а ур-нь смерт-ти в этих случаях невелик.

В периоды смены традиц. типа современным складываются промежут. типы, объединяющие черты уходящего и приходящего типов. Они не устойчивы и долго не живут.

 

ДЕМОГР. ВЗРЫВ (ДВ)

С позиции концепции демогр. перехода – ДВ – это резкое ускорение роста числ-ти н-я из-за установления промежуточного типа воспр-ва. Как правило в этот период $ смерт-ти значительно опережает $ рождаемости, что и приводит к ускорению # числ-ти н-я. ДВ – временное явл-е. По мере развития демогр. перехода нарушенная согласованность типов рожд-ти и смерт-ти востанав-ся, промежут. тип сменяется основным и ДВ прекращается. Выделяют 3 типич. схемы развития демогр. перехода:

1. обсуждение ДВ - смена типов рожд-ти и смерт-ти идет параллельно (Франция 19в.)

(схема – исключение из общ. правила)

Δе

 

рожд.

 

 

смер.

 

 

1. малый ДВ – снижение рожд-тит отстает от снижения смерт-ти на несколько десятков лет (30-40) (страны Зап. Европы 20в.). Схема типична для большинства европ. стран. За 50 лет демогр. перехода в странах зап. европы н-е этих стран почти удвоилось, но такой вид демогр. перехода имел регион. значение и не смог оказать существ. влияния на темпы роста мирового н-я.

 

1. большой ДВ – массов. снижение рожд-ти намного отстает от снижения смерт-ти. (развивающ. страны Азии, Африки, Лат. Америки – ДВ в этих странах перерос в мировой). По прогнозам ДВ в таких странах прекратится не ранее сер.21в.