Поэтому можно условно считать, что
S(x) – это численность людей в возрасте x+0,5 лет (при условии что в возрасте x смертные случаи будут равномерно распределяться по месяцам и дням жизни. Это условие справедливо для всех возрастов, кроме возраста до 1 года; x=0).
Кроме показателя l(x) - числа доживающих до точного возраста x, в таблицах смертности используется показатель среднего
числа живущих в возрасте x - L(x). Для всех возрастов от 1 года и старше среднее число живущих (в учебниках по демографии прилагательное "среднее" опускается) - это среднее арифметическое между числом
доживающих до возраста x и числом доживающих до следующего возраста x+1.
L(x)= 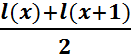
В возрасте до 1 года (x=0)
L(x)= 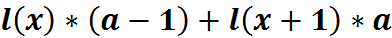
Где a – тот же параметр, который используется при расчете коэффициента смертности детей в возрасте до 1 года.
Если x=0 и
a = 0,85, то
L(0)= 
Можно считать, что L(x) - это число доживающих до возраста x+0,5 лет.
По своему смыслу именно показатель L(x) в таблицах смертности соответствует показателю S(x) - то есть, численности населения в возрасте x лет по данным переписи или текущей оценки возрастного состава населения.
d(x)
показатель d(x) из таблицы смертности, то есть число умерших в возрасте x из 100000 родившихся, то есть из исходной численности условного поколения в этой таблице, соответствует показателю M(x), то есть числу умерших в возрасте x в реальном населении.
d(x)/L(x)= mۥ(x)=M(x)/S(x)(формула обратного перехода)
L(x)=(l(x)+l(x+1))/2=
Однако l(x+1)= l(x)-d(x)