IV. Теорема о среднем

Замечание.

 

Согласно свойству 8 можно рассматривать интегралы неопределенные в ограниченном числе точек

До этого надо доопределить функцию в точке

,

 

Пусть 1. 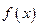или

2. - сохраняет знак на отрезке , .

Сохраняет знак на отрезке монотонности.

Тогда :

(1)

и

Так как функция 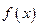классу интегрируемых функций, то эта функция ограничена на отрезке

и

Положим, что и

, тогда

Проинтегрируем на

(2)

(3)

Разделим (2) на

Введем обозначение:

(*)

Возможны 2 варианта. Из свойства (6)

А)

Тогда соотношение (1) будет выполнено для любых

Б) , где (1)

Следствие А

Пусть и сохраняет знак

: ()

Условие свойства (9) выполнено

(1)

,то по теореме о промежуточных значениях на отрезке функций

Следствие В

:,

Что имеет место:

(4)

Доказательство следует из свойства (9),если положить

Следствие С

Пусть

(5)

Доказательство следует из доказательства следствия. А если положить .