Коэффициент динамичности при ударе по безмассовой упругой системе.
Вертикальный удар. Предположим, что груз весом 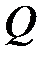 падает с некоторой высоты
падает с некоторой высоты 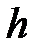 на упругую систему, масса которой мала по сравнению с массой груза. Упругую систему будем считать невесомой. Такой системой может быть стержень, балка, ферма и т. д.
на упругую систему, масса которой мала по сравнению с массой груза. Упругую систему будем считать невесомой. Такой системой может быть стержень, балка, ферма и т. д.
Рассматривая баланс кинетической и потенциальной (энергии упругой деформации) энергий в момент наибольшей деформации системы при ударе, можно получить выражение для коэффициента динамичности
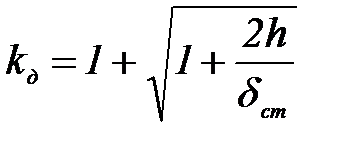
| (1.7), |
где 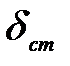 - статическое смещение точки удара упругой системы под действием силы веса
- статическое смещение точки удара упругой системы под действием силы веса 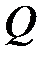 и по ее направлению.
и по ее направлению.
После нахождения 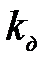 , могут быть определены динамические напряжения и деформации системы, которые, очевидно, будут в
, могут быть определены динамические напряжения и деформации системы, которые, очевидно, будут в 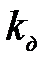 раз больше тех, которые имели бы место в системе при статическом приложении к ней груза
раз больше тех, которые имели бы место в системе при статическом приложении к ней груза 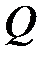 . Заметим, что эластичные свойства системы, как видно из формулы (1.7) смягчают удар и, наоборот, сила удара тем больше, чем больше жесткость системы.
. Заметим, что эластичные свойства системы, как видно из формулы (1.7) смягчают удар и, наоборот, сила удара тем больше, чем больше жесткость системы.
Другой, более общий вид формулы для коэффициента динамичности можно получить, записывая работу веса груза при ударе как сумму: 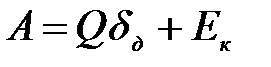 , где
, где 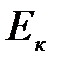 - кинетическая энергия груза к моменту удара. Тогда получим выражение:
- кинетическая энергия груза к моменту удара. Тогда получим выражение:
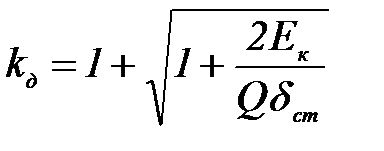
| (1.8). |
Выражая кинетическую энергию груза 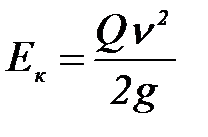 через его скорость
через его скорость 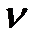 и ускорение свободного падения
и ускорение свободного падения 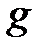 , получим еще один вариант формулы коэффициента динамичности при ударе:
, получим еще один вариант формулы коэффициента динамичности при ударе:

| (1.9). |
Частный случай ударного нагружения - внезапное приложение груза, когда 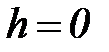 . В этом случае
. В этом случае 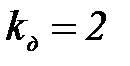 и
и 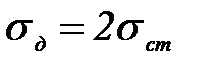 ,
,  , т. е. при внезапном приложении нагрузки напряжения и деформации системы в два раза больше, чем при статическом нагружении.
, т. е. при внезапном приложении нагрузки напряжения и деформации системы в два раза больше, чем при статическом нагружении.
Вертикальный удар вследствие внезапной остановки вертикального движения. Удар вследствие внезапной остановки движения возникает, например, в тросе лифта при внезапной остановке кабины или в балке двигающейся со скоростью 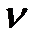 , на которой закреплен груз
, на которой закреплен груз 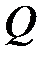 .
.
В этом случае выражение коэффициента динамичности имеет вид:
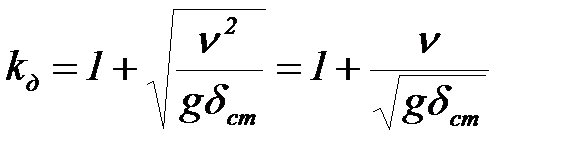
| (1.10). |
Горизонтальный удар.Рассмотрим произвольную упругую систему, по которой ударяет груз массы 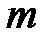 , движущийся в момент удара горизонтально со скоростью
, движущийся в момент удара горизонтально со скоростью 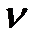 . В этом случае сила веса груза перпендикулярна перемещению и работы не совершает. В формуле (1.9) следует оставить только слагаемое, связанное с кинетической энергией груза на момент удара, и коэффициент динамичности определится выражением:
. В этом случае сила веса груза перпендикулярна перемещению и работы не совершает. В формуле (1.9) следует оставить только слагаемое, связанное с кинетической энергией груза на момент удара, и коэффициент динамичности определится выражением:
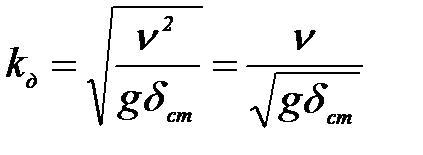
| (1.11). |
(Здесь 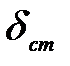 - такое перемещение точки удара упругой системы, которое она получила бы в случае статического приложения по направлению удара силы веса груза -
- такое перемещение точки удара упругой системы, которое она получила бы в случае статического приложения по направлению удара силы веса груза - 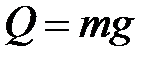 ).
).
Влияние массы ударяемой системы на коэффициент динамичности. В приведенных выше рассуждениях масса ударяемой упругой системы не учитывалась. Учет массы ударяемой системы в технической теории удара всегда приводит к снижению динамических напряжений и деформаций те есть к снижению коэффициента динамичности. Происходит это из-за того, что в момент удара груза по упругой системе, имеющей массу, система в точке удара и груз приобретают одинаковую скорость, которая по закону сохранения импульса будет меньше скорости груза до удара. При этом часть кинетической энергии груза расходуется на местную деформацию ударяемой системы и груза в месте удара.
Рассмотрим произвольную упругую систему, с закрепленной в месте удара сосредоточенной массой 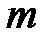 . В момент соударения груз весом
. В момент соударения груз весом 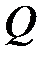 , имеющий до удара скорости
, имеющий до удара скорости 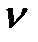 и точка удара упругой системы начинают двигаться совместно со скоростью
и точка удара упругой системы начинают двигаться совместно со скоростью 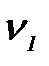 . Величина скорости
. Величина скорости 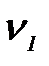 определяется из теоремы о сохранении количества движения:
определяется из теоремы о сохранении количества движения: 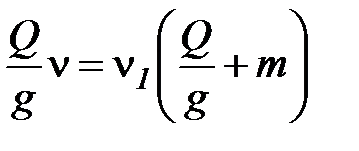
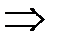
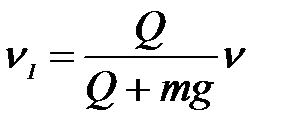 следовательно, она меньше скорости груза до удара. В этом случае при определении коэффициента динамичности можно пользоваться полученными ранее формулами (1.7-1.11), только вместо скорости груза до удара в них нужно подставить скорость
следовательно, она меньше скорости груза до удара. В этом случае при определении коэффициента динамичности можно пользоваться полученными ранее формулами (1.7-1.11), только вместо скорости груза до удара в них нужно подставить скорость 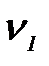 .
.
В случае, когда необходимо учесть собственную распределенную массу упругой системы ее заменяют условной сосредоточенной массой, которую называют приведенной массой системы. Величина приведенной массы зависит от распределения масс по ударяемой системе и от точки приведения (удара). Условием, из которого определяется величина приведенной массы, является равенство кинетических энергий движения распределенной массы ударяемой системы и приведенной массы после удара. Упрощенно считают, что эпюра скоростей точек ударяемой системы подобна эпюре смещений точек системы при статическом приложении веса груза.