Решение.
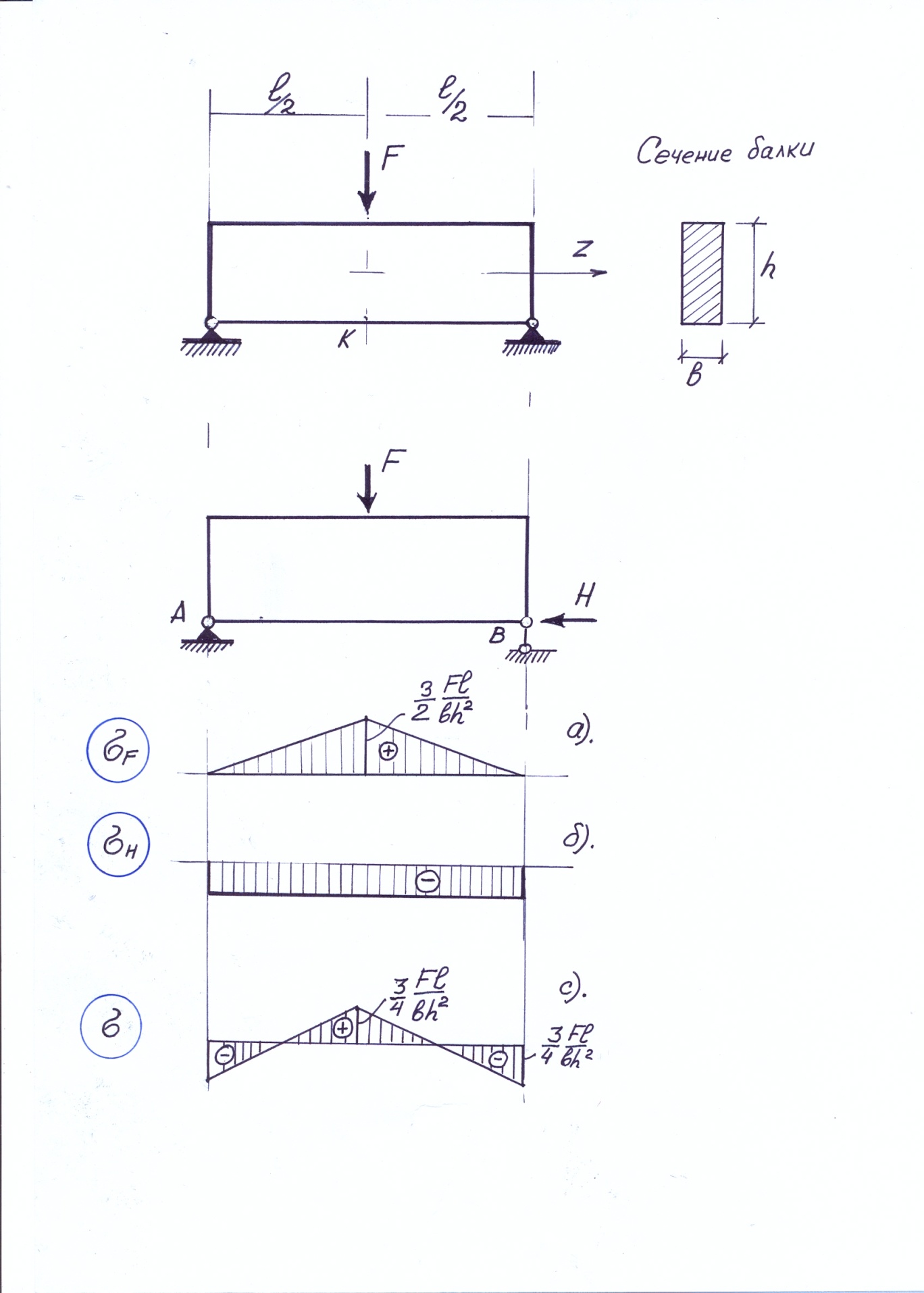
Задача является статически неопределимой (см. рис.). Можно представить, что напряжения возникают от силы 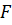 и от пока неизвестной нам горизонтальной опорной реакции
и от пока неизвестной нам горизонтальной опорной реакции  . Определим сначала напряжение в нижнем волокне от силы
. Определим сначала напряжение в нижнем волокне от силы 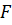 . Эта задача вполне обычная. В сечении под силой напряжение в нижнем волокне определится по формуле
. Эта задача вполне обычная. В сечении под силой напряжение в нижнем волокне определится по формуле
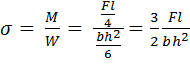 .
.
По длине нижнего волокна эпюра напряжений будет меняться также, как эпюра моментов. Таким образом эпюра в нижнем волокне только от силы 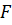 будет иметь вид, показанный на рис. а).
будет иметь вид, показанный на рис. а).
Горизонтальная опорная реакция  будет вызывать в стержне внецентренное сжатие, поэтому напряжение в нижнем волокне будет постоянным (см. рис. б)). Окончательная эпюра получится суммированием эпюр а) и б). Ординату в эпюре напряжения
будет вызывать в стержне внецентренное сжатие, поэтому напряжение в нижнем волокне будет постоянным (см. рис. б)). Окончательная эпюра получится суммированием эпюр а) и б). Ординату в эпюре напряжения  определим с таким расчетом, чтобы окончательная эпюра напряжения в нижнем волокне имела бы нулевую площадь. Соответствующая окончательная эпюра напряжений показана на рис. с).
определим с таким расчетом, чтобы окончательная эпюра напряжения в нижнем волокне имела бы нулевую площадь. Соответствующая окончательная эпюра напряжений показана на рис. с).
Теперь обоснуем то положение, что площадь окончательной эпюры напряжений 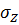 должна быть нулевой. Для этого определим упругое удлинение нижнего волокна:
должна быть нулевой. Для этого определим упругое удлинение нижнего волокна:
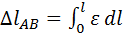 =
= 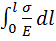 =
= 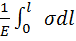 =
= 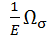 =0.
=0.
Полное удлинение отрезка А В мы приравняли нулю т.к. в точке В стоит шарнирно неподвижная опора. Таким образом обосновано принятое нами положение о том, что площадь окончательной эпюры напряжений в нижнем волокне  равна нулю. На рис. б) показана окончательная эпюра напряжений. Средняя ее ордината даст искомый ответ:
равна нулю. На рис. б) показана окончательная эпюра напряжений. Средняя ее ордината даст искомый ответ: 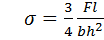 .
.
Ответ::  .
.
br>