Базовые вопросы
Классификация движения по ускорениям
1. 
. Движение прямолинейное и равномерное.
2. 
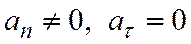. Движение криволинейное и равномерное (рис. 14).
3. 
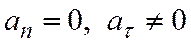. Движение криволинейное и равномерное (рис. 6).
Рис. 6
а) Прямолинейное, ускоренное (рис. 7)
Рис. 7
б) Прямолинейное, замедленное (рис. 8)
Рис.8
4. 
. Движение криволинейное и неравномерное.
а) Криволинейное, ускоренное (
) (рис. 9).
Рис. 9
б) Криволинейное, замедленное(рис. 10, а, б)
Рис. 10
\
Уравнение равномерного движения по траектории любой формы (V = const)
.
Уравнение равнопеременного движения по траектории любой формы (
= const)
,
где 
— начальное положение; 
— начальная скорость.
Если > 0 , то движение равноускоренное.
Если < 0 , то движение равнозамедленное.
Скорость равнопеременного движения
.
Задача 1.При отходе от станции поезд, двигаясь равноускоренно по закруглению радиуса 900 м, за время t = 30 с достиг скорости V= 15 м/с. Определить путь, пройденный поездом и его полное ускорение (рис. 11).
Рис. 11
Решение. За начало отсчета примем положение поезда в момент отхода от станции (рис. 11). Начальные условия движения: =0; = 0.
,
,
.
Задача 2.Поезд движется со скоростью 20 м/с. При торможении ускорение равно 0,4 м/с2. Найти время и путь торможения.
Решение. Применим формулы при начальных условиях движения
=0, = 20 м/с:
, 
.
Так как поезд остановился, то V=0, тогда
.
.
Задача 3. Точка М движется по своей траектории согласно уравнениям
х = t2 см; у = sin πt см.
Определить траекторию точки М, ее скорость и ускорение в момент времени t1 = 1,5 с. Определить касательное и нормальное ускорения, а также радиус кривизны траектории.
Решение. Для определения траектории точки М исключим из уравнений движения время, после чего получим уравнение траектории в виде
Определяем положение точки М в момент времени t1 (рис. 12)
Для определения скорости точки М вычисляем первые производные от координат по времени, равные проекциям скорости точки на соответствующие оси координат:
.
Модуль скорости определяем по формуле
.
Вычисляем проекции вектора скорости точки на оси координат и её модуль в момент времени t1
Направление вектора скорости определяем при помощи направляющих косинусов
В момент времени t1 направляющие косинусы вектора скорости
т.е. вектор скорости точки направлен параллельно оси Ох.
Для определения ускорения точки М вычисляем первые производные от проекций скорости или вторые производные от координат по времени, равные проекциям ускорения точки на соответствующие оси координат:
.
Модуль ускорения определяем по формуле
Проводим вычисления для момента времени t1
Направление вектора ускорения определяем при помощи направляющих косинусов
В момент времени t1 направляющие косинусы вектора ускорения
Для определения касательного ускорения 
точки М учтем, что его можно определить как проекцию вектора полного ускорения на направление касательной к траектории
.
В момент времени t1
м/с2.
Для определения нормальной составляющей вектора полного ускорения воспользуемся формулой
м/с2.
В данной задаче вектор касательного ускорения совпадает с проекцией вектора полного ускорения на ось Ох, а вектор нормального ускорения - с проекцией ускорения на ось Оу.
Радиус кривизны траектории определяем, используя формулу для вычисления нормального ускорения
.
В момент времени t1
м.
Изображаем все найденные величины на рис. 6.2.
Рис. 12
1. Что изучает кинематика?
2. Какие задачи решает кинематика?
3. Что называется траекторией точки?
4. Какие существуют способы задания движения точки?
5. В чем заключается естественный способ задания движения?
6. В чем заключается координатный способ задания движения?
7. Как определить скорость точки при разных способах задания движения?
8. Как определить ускорение при векторном способе задания движения?
9. Как определить ускорение при координатном способе задания движения?
10. Как определить ускорение при естественном способе задания движения?
11. Что характеризует касательное ускорение?
12. Что характеризует нормальное ускорение?