СЛОЖЕНИЕ ПОСТУПАТЕЛЬНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЙ

 

Если тело одновременно участвует в переносном поступательном движении со скоростью и относительном вращательном с угловой скоростью , то в зависимости от их взаимного расположения целесообразно рассмотреть три отдельных случая.

1. Скорость поступательного движения перпендикулярна оси относительного вращения.В этом случае векторы и перпендикулярны (рис.53). На линии ОС, перпендикулярной плоскости в которой расположены и , имеется точка С, скорость которой равна нулю. Определяем ее расстояние от точки О.

По теореме сложения скоростей для точки С имеем

,

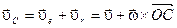так как при вращении вокруг оси

.

Учитывая, что скорости и противоположны по направлению, получим

.

Так как , то и, следовательно, точки С и О находятся на расстоянии

.

Другие точки, имеющие скорости, равные нулю, располагаются на линии, проходящей через точку С, параллельно оси вращения тела с угловой скоростью . Таким образом, имеется мгновенная ось вращения, параллельная оси относительного вращения и проходящая через точку С.

При сложении поступательного переносного и вращательного относительного движений твердого тела, у которого скорость поступательного движения перпендикулярна оси относительного вращения, эквивалентное абсолютное движение является вращением вокруг мгновенной оси, параллельной оси относительного вращения с угловой скоростью, совпадающей с угловой скоростью относительного вращения.

2. Винтовое движение.Движение, при котором скорость переносного поступательного движения тела параллельна оси относительного вращения, называется в и н т о в ы м д в и ж е н и е м т в е р д о г о т е л а (рис.54). Ось вращения тела в этом случае называется в и т о в о й о с ь ю. При винтовом движении тело движется поступательно параллельно оси винтового движения и вращается вокруг этой оси. Винтовое движение не приводится к какому-либо другому одному простому эквивалентному движению.

При винтовом движении векторы и могут иметь как одинаковые, так и противоположные направления. Винтовое движение тела характеризуется п а р а м е т р о м в и н т о в о г о г о д в и ж е н и я, которым считают величину . Если и изменяются с течением времени, то и параметры винтового движения являются переменными. В общем случае , и , т.е. p есть перемещение тела вдоль оси винтового движения при повороте тела на один радиан.

Для точки М имеем

Но , , где r – расстояние точки до винтовой оси. Скорости и перпендикулярны. Следовательно,

Учитывая, что , получаем

Если тело вращается с постоянной угловой скоростью и имеет постоянную скорость поступательного движения, то такое движение тела называется п о с т о я н н ы м в и н т о в ы м движением. В этом случае точка тела при движении все время находится на поверхности кругового цилиндра с радиусом r. Траекторией точки является винтовая линия. Кроме параметра в рассматриваемом случае вводят шаг винта, т. е. расстояние, на которое переместится какая-либо точка тела при одном обороте тела вокруг оси винтового движения. Угол поворота тела при вычисляется по формуле . Для одного оборота тела . Необходимое для этого время .

За время Т точка переместится в направлении, параллельном винтовой оси, на шаг винта .

Отсюда получается зависимость шага винта от параметра винтового движения .

Уравнения движения точки М тела по винтовой линии (рис.102) в декартовых координатах выражаются в следующей форме:

;

;

.

В этих уравнениях величины и являются постоянными.

3. Общий случай.Пусть скорость переносного поступательного движения и угловая скорость относительного вращения образуют угол . Случай когда , и , уже рассмотрены.

Разложим скорость (рис.55) на две перпендикулярные составляющие и , причем направим параллельно .

Тогда , .

Переносное движение со скоростью и относительное вращение с угловой скоростью эквивалентны вращению вокруг оси, проходящей через точку С с угловой скоростью (согласно случаю первому), причем .

Скорость поступательного движения имеют все точки тела. Таким образом, получено винтовое движение с винтовой осью, отстоящей от первоначальной оси вращения на величину .

Параметр полученного винтового движения .

Общий случай переносного поступательного и относительного вращательного движений твердого тела оказался эквивалентным мгновенному винтовому движению.