АБСОЛЮТНАЯ И ОТНОСИТЕЛЬНАЯ ПРОИЗВОДНЫЕ ОТ ВЕКТОРА. ФОРМУЛА БУРА

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ В ОБЩЕМ СЛУЧАЕ

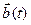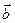Для любого вектора его производную по времени по отношению к неподвижной системе отсчета называют полной (или абсолютной) производной и обозначают . Производную по времени при учете изменения вектора относительно подвижной системы отсчета называют относительной (или локальной) производной и обозначают 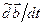или .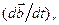

 

 

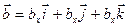
Изменение вектора Б относительно неподвижной системы координат О₁x₁y₁z₁ в зависимости от времени состоит из изменения его проекций b_х, b_у, b_z на подвижные оси координат и изменения единичных векторов , , 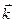подвижных осей вследствие движе­ния подвижной системы координат относительно неподвижной. Вычислим полную производную.

(*)

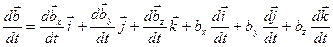Первые три слагаемых учитывают изменение вектора 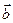при неизменных , , 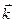и поэтому составляют относительную производную, т. е.

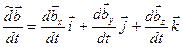
Производные по времени единичных векторов определим по формулам Пуассона

, ,

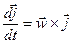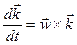
Подставляя эти зна­чения производных единичных векторов в (*) и вынося за скобки, получим

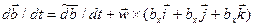
или

(**)

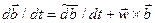Получена формула зависимости производных векторов 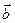в двух системах отсчета, движущихся друг относительно друга. Формула (**) называется формулой Бура.

Из формулы Бура следует, что поступательная часть движения вместе с полюсом не влияет на зависимость между производными, а влияет только вращательная часть движения.

Рассмотрим частные случаи.

1. Если вектор 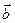не изменяется относительно подвижной системы координат, то его относительная производная 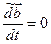и по формуле (**) получаем

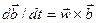
2. Если вектор 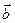не изменяется относительно основной системы координат, то полная производная 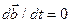и, со­гласно (**), его относительная производная

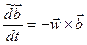
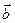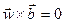3. Если , т. е. вектор все время параллелен вектору угловой скорости , то и

В частности, если , то