Функциональные ряды.

Пусть функция определена в области

Определение. Выражение

называется функциональным рядом.

Пример.

При одних значениях ряд может сходиться, для других значений – расходиться.

Пример.

Найдите область сходимости ряда 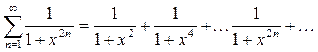. Данный ряд определен для значений

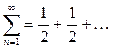Если то , ряд расходится, так как не выполняется необходимый признак сходимости ряда; если ряд расходится; если - бесконечно убывающая геометрическая прогрессия.

Сравнение данного ряда со сходящимся рядом при дает область сходимости исследуемого ряда .

При значениях из функционального ряда получается числовой ряд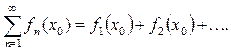

Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда.

Совокупность всех точек сходимости ряда образует область его сходимости. Областью сходимости обычно бывает какой-нибудь интервал оси .

Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области .

Сумма функционального ряда является некоторой функцией от переменной , определенной в области сходимости ряда

Какими свойствами обладают функции , если известны свойства членом ряда, то есть .

Непрерывность функций не достаточна для того, чтобы сделать заключение о непрерывности .

Сходимость ряда непрерывных функций к непрерывной же функции обеспечивается дополнительным условием, выражающим одну важную особенность сходимости функционального ряда.

Определение. Функциональный ряд называется сходящимся в области , если существует предел частичных сумм этого ряда, то есть .

Определение. Функциональный ряд называется равномерно сходящимся в области , если для любого положительного 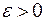, найдется такое число , что для всех выполняется неравенство .

Геометрический смысл равномерной сходимости

Если окружить график функции - полоской”, определяемой соотношением 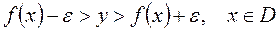то графики всех функций , начиная с достаточно большого значения , целиком лежат в этой « - полоске», окружающей график предельной функции .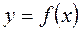

Свойства равномерно сходящегося ряда.

1. Сумма равномерно сходящегося ряда в некоторой области , составленного из непрерывных функций, является функцией непрерывной в этой области.

2. Такой ряд можно почленно дифференцировать

3. Ряд можно почленно интегрировать

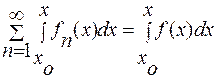Для того чтобы определить является ли функциональный ряд равномерно сходящимся, надо воспользоваться достаточным признаком сходимости Вейерштрасса.

Определение. Функциональный ряд называется мажорируемым в некоторой области изменения , если существует такой сходящийся числовой ряд 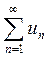с положительными членами, что для всех из этой области выполняются неравенства .

Признак Вейерштрасса (равномерной сходимости функционального ряда).

Функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

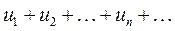Другими словами, если функции в некоторой области не превосходят по абсолютной величине соответствующих положительных чисел и если числовой ряд сходится, то функциональный ряд в этой области сходится равномерно.

Пример. Доказать равномерную сходимость функционального ряда .

Решение. . Заменим общий член этого ряда общим членом числового ряда, но превосходящего каждый член ряда по абсолютной величине. Для этого надо определить , при котором общий член ряда будет максимальным.

Тогда .

Полученный числовой ряд сходится, значит, функциональный ряд сходится равномерно согласно признаку Вейерштрасса.

Пример. Найдите сумму ряда .

Для нахождения суммы ряда воспользуемся известной формулой для суммы геометрической прогрессии

Дифференцируя левую и правую части формулы (1), получим последовательно

Выделим в сумме, подлежащей вычислению, слагаемые, пропорциональные первой и второй производной:

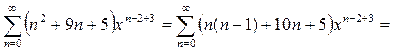
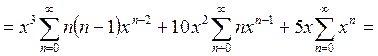
Вычислим производные:

тогда

Степенные ряды.

Среди функциональных рядов есть класс степенных и тригонометрических рядов.

Определение. Функциональный ряд вида

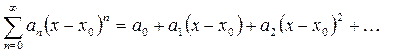
называется степенным по степеням . Выражения - постоянные числа.

Если ряд является степенным по степеням .

Область сходимости степенного ряда. Теорема Абеля.

Теорема. Если степенной ряд сходится в точке , то он сходится и притом абсолютно для всякого значения , по абсолютной величине меньшего , то есть или в интервале .

Доказательство.

Вследствие сходимости рада его общий член должен стремиться к нулю, поэтому все члены этого ряда равномерно ограничены: существует такое постоянное положительное число , что при всяком имеет место неравенство .

Тогда данный ряд можно записать так:

В силу сделанного замечания можно записать ряд

, который образует геометрическую прогрессию со знаменателем . Если , то , и прогрессия сходится. Если больший ряд сходится, то будет сходиться и данный ряд. Теорема доказана.

Следствие. Если степенной ряд расходится при значении , то ряд расходится при всяком значении , большем по абсолютной величине , .

Из теоремы Абеля и следствия из этой теоремы вытекает следующее предположение. Для каждого степенного ряда, имеющего как точки сходимости, так и точки расходимости, существует такое положительное число , что для всех , , ряд абсолютно сходится, а для значений , , ряд расходится.

Что касается значений или , то здесь возможны ситуации, когда ряд сходится в обеих точках, или только в одной из них, или ни в одной.

Определение. Число такое, что для всех , , степенной ряд сходится, а для всех , , расходится, называется радиусом сходимости ряда, а интервал называется интервалом сходимости.