Равенство
Ранее рассматривался атом особого типа терм = терм, называемый равенством, в котором используется знак равенства в инфиксной форме. Этот знак, являющийся одновременно предикатным символом, свидетельствует о том, что формула терм = терм истинна только в том случае, если оба терма соответствуют одному и тому же объекту. Обозначая константы символами X, Y, переменные символами х, у, функциональный символ символом F, это можно пояснить с помощью табл. 2.
Использование равенства можно пояснить двумя примерами из мира чудовища. Имеем формулу
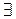(i,j)xя(3,i)
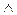хя(3,j), (3.5)
которая на естественном языке читается следующим образом: "Существуют i, j такие, что вячейках с координатами (3, i), (3, j) находится яма". Для нашего примера действительно существуют ячейки с координатами (3, 1), (3, 3), в которых находится яма. Это означает, что формула (3.5) истинна при значениях координат (3, 1), (3, 3). Значения переменных i, j могут быть как различными, так и одинаковыми. Если же используется формула (3.6) с равенством, то она будет истинна только при равных значениях i и j:
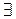(i,j)xя(3,i)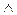хя(3,j)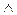(i=j), (3.6)
Формула (3.7) с отрицанием равенства, наоборот, будет истинна при различных значениях координат (3,1)
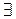(i,j)xя(3,i)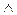хя(3,j)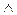
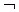(i=j). (3.7)
Таблица 2. Терм «равенство»
| Х= Y | Формула истинна, если константы Х и Y именуют один и тот же объект |
| х= Y | Формула истинна, если переменная х принимает значение, равное константе Y |
| х= у | Формула истинна, если значение переменной х совпадает со значением переменной у |
| X = F(Y) | Формула истинна, если значение функции F(Y) совпадает с константой X |
| х= F(Y) | Формула истинна, если значение функции F(Y) совпадает со значением переменной х |
| х = F(y) | Формула истинна, если значение функции F(y) совпадает со значением переменной х |
| X = F(y) | Формула истинна, если значение функции F(y) совпадает со значением константы X |