Дуговая и точечная эластичность.

Рассмотрим два метода определения ценовой эластичности спроса.

1. Дуговой метод. Обратимся к кривой спроса на рис. 2.11.

Рис. 2.11. Определение ценовой эластичности спроса.

 

Ценовая эластичность спроса будет различной на различных ее участках. Так, на участке ab спрос будет неэластичным, а на участке cd – эластичным. Измеренная на этих участках эластичность называется дуговой эластичностью.[1]

Предостережение. Одна из проблем, которая возникает при подсчете эластичности на основе изменений в количестве и цене как процентном соотношении от начальной величины (что мы проделали сейчас), состоит в том, что этот способ подсчета приводит к несоответствиям. Рост цен на 20% (с 12 ф.ст. до 14,40 ф.ст.) покрывает 20 % снижения объема продаж (с 200 до 160) и создает эластичность, равную 1 (единичную эластичность), и общий доход должен, следовательно, оставаться неизменным. Но вместо этого он уменьшается с 2400 ф.ст. (12 • 200) до 2304 (14,40 • 160) ф.ст. Почему так происходит? Это несоответствие возникает в связи с тем, что если эластичность спроса подсчитывается между двумя точками на кривой спроса, величина меняется в зависимости от того, начинаем мы считать с начальной величины или с конечной величины. Рост цены с 12 ф.ст. до 14,40 ф.ст. представляет собой 20 % изменение, равно как и уменьшение объема продаж с 200 до 160. Эластичность спроса в этом случае равна 1 (20/20). Но если мы пойдем в противоположном направлении, то получим совсем иной результат. Снижение цены с 14,40 до 12 ф.ст. сокращает объем продаж на 16,7 %, в то время как увеличение величины спроса с 160 до 200 - это изменение в 25%. В данном случае эластичность спроса равна 1,5 (25/16,7). Эластичность спроса различна в зависимости от того, с начальной или с конечной величины мы начинаем расчет. Одним из способов решения этой проблемы является расчет эластичности на основе процентного отношения средних величин или средних между двумя крайними величинами. Этот метод подсчитывает процентное изменение эластичности спроса путем деления разности конечной и начальной величин на их среднее значение. Например, 13,20 ф. ст. - есть средняя величина от двух величин - 12 ф.ст. и 14,40 ф.ст. Следовательно, согласно этому методу изменение цены с 12 ф.ст. до 14,40 ф.ст. считается ростом в 18,2%,поскольку(14,40-12)/13,20 • 100 = 18,2. Равно и изменение цены с 14,40 ф.ст. до 12 ф.ст. считается уменьшением в 18,2 %. Таким образом, метод расчета на основе средних величин дает в обоих случаях один и тот же ответ независимо от направления изменений цены. Для величины спроса средней величиной является 180. В этом случае, если величина продаж увеличивается с 160 до 200 (или уменьшается с 2 (до 160), мы считаем, что она изменилась на 22,2 % (поскольку 200-160 / 180 ·100 = 22,2). Итак, при использовании этого способа эластичность спроса по цене равна 1,22 (22/ 18,2). В данной лекции не ставится специальной задачи изучить, каким образом рассчитывается эластичность спроса по цене; для нас гораздо важнее, чтобы вы поняли взаимосвязь величины спроса и цены. Несмотря на это, данный пример показывает, что если вам необходимо подсчитать эластичность, то лучше использовать процентное отношение средней величины или средней между двумя величинами. (Добсон С., Полфреман С. Основы экономики:Минск: УП «Экоперспектива»,2004.)

Дуговая эластичность – это эластичность, измеренная между двумя точками кривой.

Фактически приведенная нами выше формула 2.8 была формулой дуговой эластичности. В числителе в ней фигурировало изменение количества блага в процентном выражении. Если мы отвлечемся от процентного выражения этого изменения и посмотрим, что есть относительное изменение Q, то нетрудно определить его как DQ/Q.[2] Аналогичным образом относительное изменение цены можно представить как DР/Р. Тогда ценовая эластичность спроса может быть представлена:

 

E_D = (2.9)

 

В качестве DQ берется разность между двумя значениями спроса на благо. Например, применительно к рис. 2.11 это могут быть разности (Q_a - Q_b) или (Q_c - Q_d). В качестве DР берется разность между двумя значениями цены, допустим (P_a - P_b) или (P_c - P_d). Проблема заключается в том, какое из двух значений количества блага и цены использовать в формуле 2.9 в качестве значений Q и Р. Понятно, что при разных значениях получается разный результат. Решение проблемы заключается в том, чтобы использовать среднее арифметическое двух значений. В таком случае мы измеряем некую среднюю эластичность на спрямляющих дуги отрезках ab и cd, и формула дуговой эластичности принимает вид:

 

E_D = ,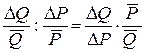

 

где = (P_a + P_b)/2 или = (P_с + P_d)/2, а = (Q_a + Q_b)/2 или = (Q_с + Q_d)/2 (опять же нижние индексы отвечают обозначениям из рис. 2.11). Если же мы рассмотрим некий общий случай и обозначим значения количеств блага и цены как Q₁, Q₂ и P₁, P₂, соответственно, то окончательно формулу дуговой эластичности после некоторых элементарных алгебраических преобразований можно представить как:

 

E_D =

 

Именно этой формулой удобнее всего пользоваться при реальных вычислениях дуговой эластичности. Конечно, для этого необходимо знать числовые значения Q₁, Q₂ и P₁, P₂.

Дуговая эластичность может рассчитываться и для случая линейной функции спроса для любых ее отрезков.

2. Точечный метод. Представим теперь, что нам нужно определить эластичность не на отрезках ab и cd, а в некоторой произвольно взятой точке f на кривой спроса (рис. 2.11). В этом случае можно воспользоваться формулой 2.9, но заменив DQ и DР бесконечно малыми величинами. Тогда эластичность можно определить как:

 

E_D = (2.10)

 

Формула 2.10 показывает точечную эластичность спроса.

Точечная эластичность – это эластичность, измеренная в некоторой точке кривой.

dQ/dP – показывает изменение спроса в ответ на изменение цены. На рис. 2.11 – это тангенс угла, образуемый касательной к кривой спроса в точке f и осью ординат (tga). Он равен –70/50 = - 1,44 (знак минус обусловлен отрицательным наклоном кривой спроса и, соответственно, касательной к ней). Относительно точки f P_f = 25, а Q_f = 35. Подставляем эти значения в формулу 2.10 и получаем, что E_D = - 1,44 × (25/35) = - 1,0. Следовательно, выше этой точки по кривой спроса спрос неэластичен, ниже – эластичен.

При изучении эластичности необходимо особо обратить внимание на то, что она лишь частично определяется наклоном кривой спроса. Это можно легко заметить на примере линейной функции спроса. С этой целью выберем знакомую нам функцию спроса Q_D = 60 - 4P и изобразим ее на рис. 2.12.

Рис. 2.12. Различные эластичности линейных функций спроса.

 

 

 

Очевидно, что у линейной функции угол наклона во всех ее точках одинаков. В нашем случае dQ/dP = tga = - 4 на всем ее протяжении. Однако в разных ее точках значение ценовой эластичности будет различным в зависимости от выбранных значений Р и Q. Так, например, в точке k эластичность равна 2, а в точке l уже только 0,5. В точке u, которая делитлинию спроса mn ровно пополам, эластичность составляет 1.

Теперь предположим, что спрос возрос так, что линия спроса сместилась в положение m¢n. Она теперь описывается функцией Q_D = 60 - 1,5P. Хорошо видно, что угол ее наклона существенно изменился. Здесь dQ/dP = tgb = - 1,5. Однако, например, в точке u¢ эластичность спроса равна - 1, как и в точке u на линии спроса mn.

Заметим, что в точке, которая делит прямую линию спроса пополам, эластичность всегда равна – 1. На отрезке выше этой точки спрос в любой точке эластичный, ниже - неэластичный в любой точке. Эти утверждения можно легко доказать, зная формулу определения эластичности и элементарную геометрию.

До сих пор мы стремились показать, что значения ценовой эластичности спроса различны для различных участков и точек линии, представляющих одну и ту же функцию спроса. Однако можно указать на три исключения, когда эластичность одинакова для всей кривой спроса. Во-первых, нетрудно заметить, что когда последняя представлена вертикальной прямой линией (рис. 2.13, график А), то эластичность спроса равна 0 (т.к. dQ/dP = 0). Такой спрос называют абсолютно неэластичным.

Рис. 2.13. Графики функций спроса с постоянными эластичностями.

 

Во-вторых, если кривая спроса представлена горизонтальной прямой линией (рис. 2.13, график Б), то эластичность спроса равна бесконечности (т.к. dQ/dP = ). Такой спрос называют абсолютно эластичным.

И, наконец, в-третьих, когда кривая спроса представлена правильной гиперболой (рис. 2.13, график В), т.е. Q_D = 1/P. Используя формулу 2.10 можно установить, что ее эластичность постоянна и равна - 1, т.е. |E_D| = 1.[3]