Введение

Содержание

Введение 4

Центральное растяжение и сжатие 5
Геометрические характеристики сечений 19
Кручение 23
Плоский поперечный изгиб 32
Неразрезные балки 75
Сложное сопротивление 97
Устойчивость 115
Динамика 123
Приложение 133

Введение

Учебное пособие содержит подробное решение типовых задач по курсу «Сопротивление материалов». Рассмотрены расчеты прямого бруса при различных видах деформации, включены задачи на кручение, устойчивость и динамическое действие нагрузки. Уделено внимание решению статически неопределимых стержневых систем и неразрезных балок.

Данное издание позволит выработать навыки в решении задач курса и облегчит самостоятельную работу студентов строительных специальностей при выполнении расчетно-проектировочных заданий.

1. ЦЕНТРАЛЬНОЕ РАСТЯЖЕНИЕ И СЖАТИЕ.

З а д а ч а 1.1.

Ступенчатый стержень находится под действием внешних сил F. Материал стержня – сталь с модулем продольной упругости E=200 ГПа.

Требуется: построить эпюры продольных сил, напряжений и перемещений. Собственный вес стержня не учитывать.

F₁=60 кН,

F₂=20 кН,

F₃=100 кН,

F₄=30 кН,

А₁=6 см²,

А₂=12 см²,

А₃=10 см²,

а=80 см,

в=100 см,

с=100 см.

Рис. 1.1. Схема стержня.

Решение.

Для определения внутренних усилий разбиваем стержень на участки. Границами участков являются точки продольной оси, соответствующие изменению площади поперечного сечения и местам приложения сосредоточенных сил. Определяем, что стержень необходимо разбить на пять участков.

Проведем сечение I-I (рис.1.2а). Отбросим нижнюю часть стержня и её действие заменим нормальной силой N₁. Запишем уравнение равновесия, проецируя все силы на ось стержня:

, откуда

На участке 1-2 нормальная сила N₁ постоянна по величине.

Проведем сечение II-II (рис.1.2б) и, отбрасывая верхнюю часть стержня, заменяем её действие нормальной силой N₂. Проецируем все силы на ось стержня:

, откуда

Аналогично находим нормальные силы в сечении III-III (рис.1.2в):

, откуда

В сечении IV-IV (рис.1.2г):

, откуда

и в сечении V-V (рис.1. 2д):

Рис.1.2. Схема расчета стержня.

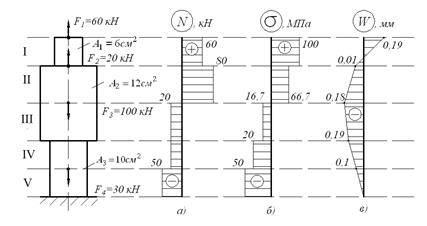
Рис.1.3.Эпюры нормальных сил, напряжений и перемещений.

Откладывая в масштабе значение нормальных сил N₁, N₂, N₃, N₄, N₅ в пределах соответствующих участков, получаем эпюру нормальных сил (рис.1.3а). Знак “плюс” показывает, что в пределах данного участка – растяжение, а “минус” – сжатие. Для построения эпюры нормальных напряжений, воспользуемся формулой:

Определим напряжение для каждого участка:

В масштабе откладываем значение напряжений и определяем, что максимальное значение напряжения достигает на участке I (рис.1.3б).

Для построения эпюры перемещений воспользуемся формулой:

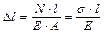Расчёт начинаем с участка V, так как перемещение в заделке отсутствует. Определим изменение длин каждого из участков:

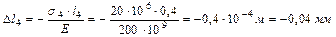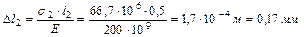Перемещение участка V: ,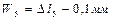

участка IV: ,

участка III: ,

участка II: ,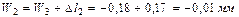

участка I: .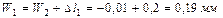

В масштабе откладываем значение перемещений (рис.1.3в).

З а д а ч а 1.2.

Конструкция, состоящая из элементов большой жёсткости и двух стальных стержней с расчетным сопротивлением материала R=210 МПа и модулем продольной упругости E=210 ГПа, загружена согласно схеме (рис.1.4).

Требуется: подобрать диаметр стержней и выполнить проверочный расчет жёсткости, если перемещение точки C не должно превышать 20 мм.

F=20кН,

q₂=10кН/м,

q₁=5кН/м,

а=0,8м,

в=1м,

[ ]=20мм.
Рис. 1.4. Схема стержневой системы.

Решение.

Для определения усилий в стержнях мысленно разделим стержневую систему на две составляющих. В первую очередь рассмотрим жёсткий элемент I (рис.1.5), так как при рассечении стержня 1 он теряет первоначальную форму равновесия. Приложим к стержню 1 неизвестную нормальную силу N₁ и определим ее значение.

Составим уравнение равновесия:

; ,

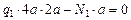Рис.1.5. Схема жесткого элемента I.

Определим опорные реакции Y_A и X_A, составив уравнения равновесия:

ΣY=0, ,

Знак «минус» показывает, что направление реакции необходимо заменить на противоположное.

ΣX=0, следовательно, X_A=0.

Рассмотрим жесткий элемент II (рис.1.6), приложив к нему нормальную силу N₁, взятую с обратным знаком. Рассечем стержень 2, приложив к нему усилие N₂.

Рис.1.6. Схема жесткого элемента II.

Cоставим уравнение равновесия:

, ,

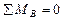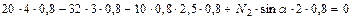Определим sin . Длина стержня 2 равна:

тогда ,

Подберём диаметр сечения для стержней по расчетному сопротивлению R:

, .

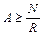Для первого стержня:

, ,

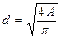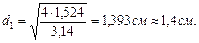
Для второго стержня:

Определим опорные реакции Y_B и X_B , составив уравнения равновесия:

ΣY=0, F – N₁ – q₂·a + N₂·sinα + Y_B = 0,

Y_B = -20 + 32 + 10·0,8 + 54,44·0,529 = - 8,79 кН.

ΣX=0, X_B + N₂·cosα = 0, X_B = - N₂·cosα,

X_B = - 54,44·0,847= - 46,09 кН.

Знак «минус» свидетельствует о том, что направление реакций Y_B и X_B необходимо заменить на противоположное.

Для проведения расчёта на жёсткость, определим удлинение стержней 1 и 2 (рис.1.7):

Составим схему перемещений элементов стержней системы, предположив, что жёсткие брусья будут поворачиваться относительно своих опор, оставаясь прямыми (рис.1.7).

Из-за малости перемещений будем полагать, что точки D, E и K, переместятся соответственно в точки D'',E' и K', т.е. перемещения абсолютно жёстких брусьев будет происходить вертикально.

Определим перемещение точки D:

Рис. 1.7. Схема перемещений стержневой системы.

Из подобия треугольников BEE' и BDD' определим перемещение точки Е:

, .

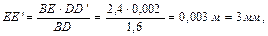
Из подобия треугольников АСС'' и АKK'' определим перемещение точки С:

Жёсткость конструкции обеспечена.

З а д а ч а 1.3.

Конструкция, состоящая из элементов большой жёсткости и двух стальных стержней с расчётным сопротивлением материала R=210 МПа и модулем продольной упругости Е=210 ГПа, загружена согласно схеме (рис. 1.8).

Требуется: подобрать диаметр стержней и выполнить проверочный расчёт жёсткости, если перемещения точки С не должно превышать 20 мм.

F=20 кН, а=1 м,

q=12 кН/м, b=1,5м, [δ] = 20 мм.

Рис. 1.8. схема стержневой системы.

Решение.

Определим усилия в стержнях, мысленно разделив стержневую систему на 2 составляющих. Рассмотрим жёсткий элемент I

(рис.1.9).

Приложим к стержню 1 неизвестную нормальную силу N₁ и определим ее значение, составив уравнение равновесия:

Определим реакцию в шарнире Y_C:

Рис. 1.9. Схема жесткого элемента I.

Рассмотрим жёсткий элемент II (рис.1.10), приложив к нему реакцию Y_C, взятую с обратным знаком.

return false">ссылка скрыта

Рис. 1.10. Схема жесткого элемента II.

Рассекаем стержень 2 и прикладываем к нему усилие N₂.

Cоставим уравнение равновесия:

тогда ,

где

Подберём диаметр сечения для стержней по расчётному сопротивлению R:

Для первого стержня:

Для второго стержня:

Определим опорные реакции X_В и Y_В, составив уравнение равновесия:

ΣY=0, Y_B - q·4a + N₂·sinα + R_C = 0,

ΣX=0, -X_B + N₂·cosα = 0, X_B = 66,67·0,8=53,34 кН.

Для проведения расчёта на жёсткость, определим удлинение стержня 2 (рис.1.11):

Перемещение точки С в положении С' определяется только удлинением стержня 2. Из подобия треугольников BCC' и BDD'':

Рис. 1.11. Схема перемещений стержней системы.

Жёсткость конструкции обеспечена.

З а д а ч а 1.4.

Система, состоящая из элементов большой жёсткости и двух стальных стержней, загружена расчётной нагрузкой (рис.1.12). Расчётное сопротивление материала стержней R=210 МПа.

Требуется: проверить прочность стержней.

q=10 кН/м,

F=20 кН,

A₁=5 см²,

A₂=10 см²,

а=2 м.

Рис. 1.12. Схема стержневой системы.

Решение.

Рис. 1.13. Схема стержневой системы с нагрузкой.

Составим расчётную схему стержневой системы (рис. 1.14).

Рис. 1.14.Расчетная схема стержневой системы.

В схеме N₁ и N₂ – нормальные силы, возникающие в стержнях ВВ₁ и СС₁, Y_o и X_o – вертикальная и горизонтальная составляющая опорной реакции шарнирно-неподвижной опоры О. Таким образом, имеем 4 неизвестные реакции (N₁, N₂, Y_o, X_o) и три уравнения равновесия ( Следовательно, данная система является один раз статически неопределимой и для её решения требуется составить дополнительное уравнение перемещений.

Запишем уравнение равновесия:

Данное уравнение имеет 2 неизвестные нормальные силы.

Для составления дополнительного уравнения перемещений рассмотрим деформацию системы, предположив, что абсолютно жёсткий элемент BOC при деформации повернётся вокруг опоры О, оставаясь жёстким.

Составим схему перемещений (рис.1.15).

Рис. 1.15. Схема перемещений стержневой системы.

Из подобия треугольников ОСС' и ОВВ' определим: . Т.к. ОС=ОВ=6м, следовательно

Примем, что А₁=А, тогда А₂=2А.

Рассчитаем длину стержней:

Решаем систему уравнений:

Определим напряжение в стержнях:

Прочность стержней обеспечена.

Определим опорные реакции в точке О:

ΣY=0, Y_O - q·2a + N₂·sin45^o – N₁·cos60^o = 0,

Y_O = 10·4 + 6,974·0,707 - 2·0,5 = 43,93 кН,

ΣX=0, -X_O + N₁·sin60^o + N₂·cos45^o = 0,

X_O = 2·0,866 + 6,974·0,707 = 6,663 кН.

2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ СЕЧЕНИЙ.

З а д а ч а 2.1.

Для заданного сечения (рис.2.1), состоящего из прямоугольного листа и прокатных профилей требуетcя: вычислить главные центральные моменты инерции, начертить сечение и показать все оси и размеры.

1. Лист 22 2см,

2. Уголок неравнобокий 125 80 8,

3. Двутавр №18.

Рис. 2.1. Схема сечения.

Решение.

Предварительно рассчитаем и выпишем из сортамента (Приложение 1) геометрические характеристики профилей, составляющих сечение.

Геометрические характеристики листа (фигура 1):

см²,

Геометрические характеристики уголка (фигура 2):

Уголок в составном сечении повернут на 90^о, поэтому моменты инерции из сортамента меняются местами. Геометрические характеристики двутавра (фигура 3):

Определим положение центра тяжести сечения, предварительно выбрав вспомогательные оси x_o и y_o. Проведем эти оси через центр тяжести листа и рассчитаем расстояние между осями x_o и y_o и центральными осями каждого из элементов сечения (рис.2.2).

Рис. 2.2. Схема составного сечения с положением главных центральных осей (размеры даны в см).

Через центр тяжести фигуры проводим центральные оси x_c и y_c.

Рассчитаем расстояния между осями x_c и y_c и центральными осями каждого из элементов сечения. Расстояния между осями x_i:

a₂= 2,84 - 2,26=0,58 cм, a₃= -10 - 2,26= - 12,26 см.

Расстояния между осями y_i:

Определим осевые моменты инерции составного сечения относительно центральных осей:

Определим центробежный момент инерции составного сечения, предварительно вычислив центробежный момент инерции уголка:

Перед корнем принят знак «минус», т.к. ось I_min уголка повернута по отношению к оси y₂ против часовой стрелки.

Центробежный момент инерции всего сечения:

т.к. фигуры имеют оси симметрии.

Определим положение главных центральных осей сечения:

Угол откладывает от оси x_c по ходу часовой стрелки (рис.2.2).

Определим значение главной центральных осей составного сечения:

Проверим правильность вычисления:

5134,97+3057,43=7737,54+454,86.

3.КРУЧЕНИЕ.

Задача 3.1.

Стальной вал круглого поперечного сечения нагружен скручивающими моментами. Расчётное сопротивление материала вала на сдвиг R_c=130 МПа, а модуль сдвига G=80 ГПа.

Требуется:

1) подобрать диаметр вала;

2) построить эпюру крутящих моментов и напряжений;

3) построить эпюру углов закручивания;

4) построить эпюру относительных углов закручивания.

Рис. 3.1 Схема вала.

а=1м, в=0,8м, с=1,2м,

Рис 3.2.Эпюры крутящих моментов, касательных напряжений, углов закручивания и относительных углов закручивания.

Построим эпюру крутящих моментов.

При определении крутящих моментов в сечениях вала, принимаем следующее правило знаков: момент считается положительным, если при взгляде со стороны сечения его направление совпадает с движением часовой стрелки.

Участок АВ:

Участок ВС:

Участок СD:

Участок DE:

По эпюре определяем максимальный крутящий момент:

Определим диаметр вала из условия прочности.

где ;

м.

Определим диаметры вала из условия жесткости.

где рад.

м.

Из двух значений диаметров выбираем большее, округлив до 0,09м: .

Определим касательные напряжения, действующие в сечениях.

Участок АВ. Па=83,88МПа.

Участок ВС:

Па=-62,91МПа.

Участок СD:

Па=-6,99МПа.

Участок DE:

Па=-118,82МПа.

Построим эпюру касательных напряжений (рис.3.2б).

Определим углы закручивания на участках вала. Используем следующую формулу:

;

, т.к. угол поворота в заделке отсутствует.

рад,

Построим эпюру углов закручивания (рис.3.2.в).

Определим относительные углы закручивания на участках вала. Для расчета используем формулу ;

Построим эпюру относительных углов закручивания (рис.3.2.г) Наиболее загруженным является участок DE, где

Условие прочности выполняется.

Задача 3.2.

Требуется:

5) подобрать диаметр вала;

6) построить эпюру крутящих моментов и напряжений;

7) построить эпюру углов закручивания;

8) построить эпюру относительных углов закручивания.

а=1,2м; в=1,4м; с=0,9м;

Рис. 3.3.Схема вала. Эпюры крутящих моментов, касательных

напряжений, углов закручивания и относительных углов

закручивания.

Построим эпюру крутящих моментов. Выберем начало координат в точке А, предположив, что вал имеет защемление в этой точке.

Определим величину уравнения неизвестного момента , составив уравнение равновесия:

Участок АВ:

Участок ВС:

УчастокCD:

УчастокDE:

По эпюре ( рис 3.3а) определяем максимальный крутящий момент:

Определяем диаметр вала из условия прочности.

где ,

Определим диаметр вала из условия жесткости.

, где

Из двух значений диаметров выберем большее, округлив до 0,11м.

Определим касательные напряжения, действующие в сечениях.

Участок АВ:

Участок ВС:

Участок СD:

Участок DE:

Построим эпюру касательных напряжений (рис. 3.3б).

Определим углы закручивания на участках вала. Используем формулу:

, (приняли в условии задачи, что т. А является неподвижной).

Построим эпюру углов закручивания (рис. 3.3в).

Определим относительные углы закручивания на участках вала.

Для расчета используем формулу

Построим эпюру относительных углов закручивания (рис 3.3г).

Наиболее загруженным является участок ВС, .

Условие прочности выполняется.

4. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ.

З а д а ч а 4.1.

Для указанной балки построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать двутавровое сечение из прокатного профиля, если R=210 МПа, R_c=130 МПа.

m=20 кН·м, q=8 кН/м, F=12кН.

Решение.

Определим реакции опор. Составим уравнение равновесия:

Рис. 4.1. Схема балки. Эпюры поперечных сил и изгибающих

моментов.

Исходя из направления нагрузок ( ) определяем, что горизонтальная реакция равна нулю.

Построим эпюры поперечных сил и изгибающих моментов методом сечений.

В точке А:

В точке В:

В точке С (правее):

В точке С (левее):

В точке D:

Подберём двутавровое сечение при R=210 МПа.

Максимальный изгибающий момент M_max определим по эпюре изгибающих моментов (рис.4.1). M_max = 170,08 кН·м.

Пользуясь сортаментом (Приложение 1), выбираем двутавр №40 с W_x=953 см³.

Проверим прочность по нормальным напряжениям:

Недогрузка составляет:

Проверим прочность по касательным напряжениям:

Максимальное значение поперечной силы (Q_Y _max) определяем по эпюре поперечных сил (рис.4.1).

(геометрические характеристики выбираем из Приложения 1).

Прочность двутавровой балки по нормальным и касательным напряжениям обеспечена.

З а д а ч а 4.2.

Для указанной балки (рис.4.2) построить эпюры внутренних усилий. Подобрать сечение из двух швеллеров из прокатных профилей, если R=210 МПа, R_c=130 МПа.

m=18 кН·м, q=20 кН/м, F=12кН.

Рис. 4.2. Схема балки. Эпюры поперечных сил и изгибающих

моментов.

Решение.

Определим реакции опор. Составим уравнение равновесия:

Проверим правильность определения реакций:

Построим эпюры поперечных сил и изгибающих моментов методом сечений (рис.5.2).

В точке А:

В точке В (левее):

В точке В (правее):

В точке С (левее):

В точке С (правее):

В точке D(левее)

В точке Е эпюра поперечных сил пересекает ось z. Определим значение изгибающего момента в этой точке. Определим расстояние Z₀:

Подберём сечение в виде двух швеллеров (Приложение 2) при R=210 МПа.

(из эпюры М, рис.4.2).

Для одного швеллера: Из сортамента (Приложение 2) выбираем швеллер №24 с W_x=242 см³. Для двух швеллеров W_x=

Проверим прочность по нормальным напряжениям:

МПа.

Перегрузка составляет:

Проверим прочность по касательным напряжениям:

(геометрические характеристики швеллера выбираем из Приложения 2).

Прочность балки, состоящей из двух швеллеров, по нормальным и касательным напряжениям обеспечена.

З а д а ч а 4.3.

Для указанной балки построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать прямоугольное сечение из древесины, если соотношение сторон сечения составляют

m=8 кН·м, q=6 кН/м, F=8кН.

Рис. 4.3. Схема балки. Эпюры поперечных сил и изгибающих

моментов.

Решение.

Определим реакции опор. Составим уравнение равновесия:

Проверим правильность определения реакций:

Построим эпюры поперечных сил и изгибающих моментов (рис.5.3):

В точке А:

В точке В (левее):

В точке В (правее):

В точке С (левее):

В точке С (правее):

В точке D:

Подберём прямоугольное сечение,

(рис 4.3),

Округляем см, тогда см,

<16 МПа.

Недогрузка составляет:

Проверим прочность по касательным напряжениям:

(из эпюры поперечных сил, рис 4.3).

Прочность деревянной балки по нормальным и касательным напряжениям обеспечена.

З а д а ч а 4.4.

Для указанной балки (рис.5.4) построить эпюры внутренних усилий. Выполнить расчёт на прочность. Подобрать круглое сечение из древесины, если R=16 МПа, R_C=2 МПа,

m=20 кН·м, q=10 кН/м, F=16кН.

Решение.
Определим реакции опор. Составим уравнение равновесия:

Рис.4.4. Схема балки. Эпюры поперечных сил и изгибающих моментов.

Проверим правильность определения реакций:

Построим эпюры поперечных сил и изгибающих моментов.

В точке А:

В точке В (левее):

В точке В (правее):

В точке С (левее):

В точке С (правее):

В точке D:

Определим значение изгибающего момента в точке K и М (в этих точках эпюра поперечных сил меняет знак).

Подберём круглое сечение. Из эпюры изгибающих моментов (рис.4.4) выберем максимальный изгибающий момент.

Принимаем

Определим максимальные нормальные напряжения:

Проверим прочность по касательным напряжениям:

(из эпюры поперечных сил,

рис.4.4)

Прочность деревянной балки по нормальным и касательным напряжениям обеспечена.

З а д а ч а 4.5.

Для указанной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки – двутавр № 30, R=210 МПа, R_C=130 МПа,

m=24 кН·м, q=16 кН/м, F=18кН.

Рис.4.5. Схема шарнирной балки. Эпюры поперечных сил и изгибающих моментов.

Решение.

Данная шарнирная балка может рассматриваться как сочетание консольной балки DE и подвесной двухопорной балки AD, для которой правой опорой является конец консоли D первой балки.

Рассмотрим равновесие подвесной балки AD и определим ее опорные реакции:

Определим правильность определения опорных реакций:

Построим эпюры поперечных сил и изгибающих моментов.

В точке А:

В точке В (левее):

В точке В (правее):

В точке С (левее):

В точке С (правее):

В точке D:

Рассмотрим консольную балку DE. Реакцию Y_D прикладываем в точке D с противоположным знаком. Строим эпюры поперечных сил и изгибающих моментов с учётом Y_D.

В точке D:

Определим величину изгибающих моментов в точках K и M (в данных точках эпюра поперечных сил меняет знак, рис.4.5):

Проверим прочность балки по нормальным напряжениям:

Недогрузка составляет:

Проверим прочность балки по касательным напряжениям:

- все геометрические характеристики двутавра № 30 выбираем из сортамента (Приложение 1).

Прочность двутавровой балки по нормальным и касательным напряжениям обеспечена.

З а д а ч а 4.6.

Для указанной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки – двутавр № 24, R=210 МПа, R_C=130 МПа,

m=10 кН·м, q=12 кН/м, F=20кН.

Рис.4.6. Схема шарнирной балки. Эпюры поперечных сил и изгибающих моментов.

Решение.

Данная шарнирная балка может рассматриваться как сочетание балки AD, лежащей на двух опорах и подвесной двухопрной балки DE.

Рассмотрим равновесие подвесной балки DE. Определим реакции опор:

Проверяем правильность определения реакций опор:

Построим эпюры поперечных сил и изгибающих моментов на участке DE шарнирной балки.

В точке Е:

В точке D:

Определим реакции опор балки AD, приложив в точку D реакцию Y_D, взятую с обратным знаком.

Проверяем правильность определения реакций опор:

Построим эпюры поперечных сил и изгибающих моментов на участке AD шарнирной балки.

В точке D:

В точке С (правее):

В точке С (левее):

В точке В (правее):

В точке В (левее):

В точке А:

Определим координаты точек К и М (z_k и z_m) :

Вычислим значение изгибающих моментов в точках K и М:

Проверим несущую способность балки:

Для двутавра № 24 из сортамента (Приложение 1) выпишем значение момента сопротивления: (из эпюры изгибающих моментов, рис.5.6).

Прочность балки по нормальным напряжениям обеспечена.

Проверим прочность балки по касательным напряжениям:

Для двутавра № 24 выпишем из сортамента (Приложение 1) геометрические характеристики сечения:

Прочность балки по касательным напряжениям обеспечена.

З а д а ч а 4.7.

Для указанной шарнирной балки построить эпюры внутренних усилий и проверить прочность. Поперечное сечение балки - двутавр № 24, R=210 МПа; R_C=130 МПа,

m=16 кН·м, q=8 кН/м, F=12кН.

Решение.

Данная балка может рассматриваться как сочетание балок КЕ, ЕС, последовательно лежащих на консоли АС.

Рассмотрим равновесие подвесной балки КЕ. Определим реакции опор: