Метод экономико-математического моделирования
Моделированиепредставляет собой процесс изобретения и написания модели, отражающей происходящие явления и процессы в экономической жизни общества.
Любое явление в жизни можно описать словами, изобразить графически или таблично, а также попытаться вывести закономерность его проявления в математической форме. В качестве простейшего примера можно привести модель круговых потоков, которая будет рассмотрена в данной теме.
В целом можно сказать, что экономическая модель представляет собой описание функциональных связей между экономическими явлениями.
Она может быть представлена:
§ таблично
§ в виде графика
§ в виде системы уравнений.
Если в области естественных и технических наук моделирование, как правило, основывается на материальной аналогии объекта исследования и модели, то в области экономических наук – на аналогии мысленной.
Процесс создания моделей включает в себя последовательное выполнение следующих этапов (рис. 1.1):
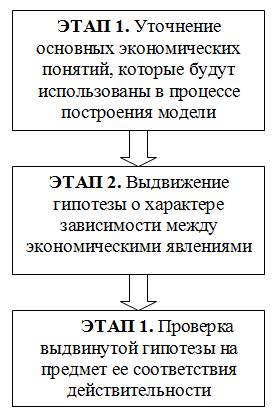
Рис. 1.1. Процесс создания экономико-математической модели
Модель включает два типа переменных:
· эндогенные - это переменные, вероятностное значение которых определяется с помощью модели;
· экзогенные - это переменные, которые принимаются как нечто заданное извне.
Построить модель функционирования системы ‒ это значит отыскать функцию, связывающую эндогенные и экзогенные переменные.
Выводы модели даются в виде гипотезы, достоверность которой невозможно четко проверить. Поэтому макроэкономические модели включают систему допущений, а следовательно являются упрощенным отражением действительности. Тем не менее, несмотря на высокий уровень абстракции, они позволяют сосредоточиться на основных элементах экономической системы, их взаимосвязях и служат теоретической основой для разработки государственной экономической политики.
Макроэкономика объединяет множество самых разных моделей: модель круговых потоков, модели товарного рынка (модель «доходы-расходы» Кейнса, модель AD-AS, модель IS), модели денежного рынка (модель LM, модель IS-LM), общего экономического равновесия и др.