Момент инерции относительно центральной оси называется центральным моментом инерции.

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Из формулы [1] видно, что момент инерции относительно центральной оси меньше, чем момент инерции относительно любой нецентральной оси, параллельной центральной.

2. МОМЕНТЫ ИНЕРЦИИ СЛОЖНЫХ ФИГУР

Момент инерции сложной фигуры равен сумме моментов инерции ее составных частей:

 

. (2)

 

Это непосредственно следует из свойств определенного интеграла

 

,

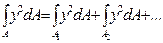где A=A₁+A₂+A₃+ . . . .

Таким образом, для вычисления момента инерции сложной фигуры надо разбить еена ряд простых фигур, вычислить мо­менты инерции этих фигур и затем просуммировать этимоменты инерции.

Указанная теорема справедлива также и для центробежного момента инерции.

Моменты инерции прокатных сечений (двутавров, швелле­ров, уголков и т. д.) приводятся в таблицах сортамента.

3. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ

Найдем зависимость между моментами инерции относитель­но осей х, у и моментами инерции относительно осей x₁, у₁, по­вернутых на угол α, (рис. 2.). Пусть I_x>I_y и положительный угол α,отсчитывается от оси х противчасовой стрелки.

Рисунок 2

Для решения поставленной задачи найдем зависимость меж­ду координатами площадки dА в исходных и повернутых осях. Из чертежа следует:

x₁=OC=OE+EC=OE+DF=ODcosα+DBsinα=xcosα+ysinα, (3)

y₁=BC=BF–DE=ycosα–xsinα. (4)

Теперь определиммоменты инер­ции относительно осей x₁ и y₁

; (5)

аналогично,

, (6)

(7)

Складывая(5)и (6), получаем

I_x1+I_y1=I_x+I_y=I_p (8)

Вычитая (5) из (6), получаем

I_x1–I_y1=(I_x–I_y)cos2α–2I_xysin2α . (9)

Формула, (8) показывает, что

сумма моментов инерции относительно любых взаимно пер­пендикулярных осей не меняется при их повороте.

Формула (9) может быть использована для вычисления центробежного момента инерции относительно осей х, у по известным осевым моментам инерции относительно осей х, y и x₁, y₁.

4. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

 

При изменении угла α I_x1 , I_y1 и I_x1y1 изменяются. Найдем значение угла, при которомI_x1, и I_y1 имеют экстремальные значе­ния. Для этого возьмем отI_x1или I_y1 первую производную по α и приравняем ее нулю:

dI_x1 /dα= – 2I_x cosα₀sinα₀ +2 I_y cosα₀sinα₀ –2 I_xy cos2α₀=0

или

(I_y – I_x) sin2α₀ –2 I_xy cos2α₀=0

откуда

tg2α₀ =2 I_xy / (I_y – I_x) . (10)

 

Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относи­тельно другой — минимален,

Такие оси называют главными. Моменты инерции относи­тельно главных осей называютсяглавными моментами инерции.

Значения главных моментов инерции найдем из формул (5) и (6), подставив в них α₀ формулы (10), при этом используем известные формулы тригонометрии для функ­ций двойных углов.

После преобразований получим следующую формулу для определения главных моментов инерции:

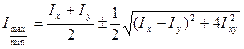(11)

Исследуя вторую производную d²I_x1 /dα² можно установить, что для данного случая (I_x>I_y) максимальный момент инерции I_max имеетместо относительно главнойоси, повернутой наугол α₀ по отношению к оси х, а минимальный момент инерции — относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфи­гурации сечений видно, какая из главных осей соответствует максимуму момента инерции.

Кроме формулы (9) для определения главных моментов инерции можно пользоваться также формулами (5) и (6), При этом сам собой решается вопрос: относительно какой главной оси получается максимальный момент инерции и относительно какой оси — минимальный?

Покажем теперь, что относительно главных осей центробеж­ный момент инерции равен нулю.

Действительно, приравнивая I_x1y1 по формуле (7) нулю, получаем

[(I_x–I_y)/2]sin2α₀ +I_xycos2α₀=0,

откуда для tg2α₀ вновь получается формула (10).

Таким образом, главными осями называютоси, обладающие следующими свойствами:

1. Центробежный момент инерции относительно этих осей равен нулю.

2. Моменты инерции относительно главных осей имеют эк­стремальные значении (относительно одной—максимум, отно­сительно другой — минимум).