Аналогично, статический момент относительно оси Оу

 

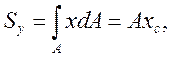(4)

откуда

x_C =S_y /A . (5)

Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.

Из формул (2) и (4) следует, что если оси x и y проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральны­ми осями. Относительно любой оси, проходящей через центр тяжести сечения (т. е. относительно любой центральной оси), статический момент равен нулю.

Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т. д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статиче­ских моментов этих простых фигур. Это непосредственно следует из свойств определенного интеграла.

Если фигура имеет ось симмет­рии, то последняя всегда проходит через центр тяжести фигуры, а по­тому статический момент фигуры от­носительно оси симметрии всегда ра­вен нулю.

Во многих случаях вместо прос­тых интегралов вида (1) и (4) удобнее иметь дело с двой­ными интегралами вида

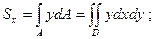(1а)

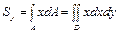. (4а)

Здесь D – область интегрирования.

2. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЯ

Осевым или экваториальным моментом инерции сечения называется геометрическая характеристика, численно равная интегралу:

относительно оси х

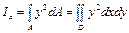; (5)

относительно оси у

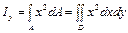, (6)

где у — расстояние от элементарной площадки dA дооси х (см. рис. 1); х— расстояние от элементарной площадки до оси у; D — область интегрирования.

Полярным моментом инерции сечения называется геометри­ческая характеристика, определяемая интегралом вида

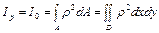, (7)

где ρ — расстояние от площадки dА до точки (полюса) (см. рис. 1), относительно которой вычисляется полярный момент инерции. Осевые и полярный моменты инерции всегда положительны.

Действительно, независимо от знака координаты произволь­ной площадки соответствующее слагаемое положительно, так как в него входит квадрат этой коор­динаты.

Центробежным моментом инерции 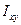сечения называется геометрическая характеристика, определяемая интегра­лом вида

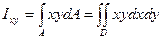, (8)

где х, у — расстояния от площадки dА до осей х и у.

Единицей момента инерции является единица длины в четвертой степени (по СИ — м⁴, хотя для прокатных профилей по ГОСТу—см⁴).

Центробежный момент инерции может быть положительным, отрицательным и в частном случае равным нулю.

Если взаимно перпендикулярные оси х и у или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю.Действительно, для симметричной фигуры всегда можно выделить два элемента ее площади (рис.2), которые имеют одинаковые ординаты у и равные, но противоположные по знаку абсциссы х. Состав­ляя сумму произведений xydA для таких элементов, т. е. вычис­ляя интеграл (8), получают в результате нуль.

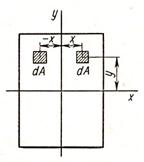
Рисунок 2

Легко доказать, что полярный момент инерции относительно какой-либо точки равен сумме осевых моментов инерции относительно двух взаим­но перпендикулярных осей, проходящих через эту точку.

Действительно, из рис. 1 видно, что ρ²=х² +у². Подста­вив это значение ρ² в выражение (7), получим

.

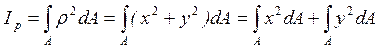Следовательно,

I_p=I_x+I_y . (9)

 

ЗАВИСИМОСТЬ МЕЖДУ МОМЕНТАМИ ИНЕРЦИИ ДЛЯ ПАРАЛЛЕЛЬНЫХ ОСЕЙ И ПРИ ПОВОРОТЕ КООРДИНАТНЫХ ОСЕЙ. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

 

1.Зависимость между моментами инерции относительно параллельных осей

Определим момент инерции фигуры относительно какой-либо оси х₁ , (рис. 1.).

Пусть x₀ — центральная ось и момент инерции I_x0 известен. Из чертежа видно, что у₁=а+у. Следовательно,

.

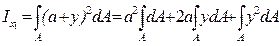Первый интеграл дает пло­щадь сечения. Второй интеграл, представляющий статический мо­мент относительно центральной оси x₀ и равен нулю.

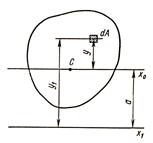
Рисунок 1

Третий интеграл представляет собой момент инерции I_x0 фигуры

относительно оси x₀. Таким обра­зом,

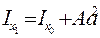. (1)