Эквивалентность ставок простого и сложного процентов. Номинальная и эффективная процентные ставки

Формулы эквивалентности позволяют определить, какая ставка простого процента соответствует заданной ставке сложного и, наоборот, какая ставка сложного соответствует ставке простого:

Формулы эквивалентности используются в:

ü расчете эффективной процентной ставки для анализа депозитных договоров;

ü расчете темпа инфляции;

ü расчете доходности спекулятивных операций с валютой и ценными бумагами.

Номинальная ставка.В современных условиях проценты капитали­зируются обычно не один, а несколько раз в году – по полугоди­ям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют даже ежедневное начисление процентов. При начисле­нии процентов несколько раз в году можно воспользоваться форму­лой 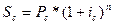, однако параметр nв этих условиях будет означать число периодов начисления, а под ставкой i_с следует понимать ставку за соответствующий период. Например, при поквартальном начисле­нии процентов за пять лет по квартальной (сложной) ставке 8% об­щее число периодов начисления составит 5 * 4 = 20. Множитель на­ращения равен 1,08²⁰ = 4,6609. На практике, как правило, в контра­ктах фиксируется не ставка за период, а годовая ставка и одновре­менно указывается период начисления процентов, например «18% годовых с поквартальным начислением процентов».

Итак, пусть годовая ставка равна j,а число периодов начисления в году равно m.Таким образом, каждый раз проценты начисляются по ставке j/m.Годовую процентнуюставку (j)называют номинальной.

Формулу наращения теперь можно представить следующим об­разом:

,

где N –общее количество периодов начисления;

j/m – ставка за период, исчисленная на основе базовой (номиналь­ной ставки j), и числа раз начисления процентов в году (m).

Если N – целое число (N = m*n), то в большинстве случаев для определения величины множителя наращения можно воспользо­ваться таблицей сложных процентов (Приложение 2). Напри­мер, при j = 20% и поквартальном начислении процентов (m = 4) в течение пяти лет отыскиваем табличное значение множителя для i = 20/4 = 5% и n = 5 * 4 = 20, находим q = 2,653298.

Чем чаще начисляются проценты, тем быстрее идет процесс наращения.

Эффективная ставка.Эффективная процентная ставкаизмеряет тот реальный относительный доход, который получают в целом за год от начисления процентов.

Эффективная процентная ставка – это годовая процентная ставка, рассчитанная по схеме сложного процента, эквивалентная заданной процентной ставке с учетом периодичности начисления процентов. Иначе говоря, эффективная ставка – это годовая ставка сложных процентов, которая дает тот же результат, что и m-разовое начисление процентов по ставке j/m.

Обозначим эффективную ставку через i_эф. По определению множи­тели наращения по двум видам ставок (эффективной и номиналь­ной при m-разовом начислении) должны быть равны друг другу:

откуда

 

Как видим, эффективная ставка при m >1 больше номинальной, при m = 1, i = j.

Замена в договоре номинальной ставки j при m-разовом начис­лении процентов на эффективную ставку i_эф не изменяет финансовых обязательств участвующих сторон, т.е. обе ставки эквивалентны в финансовом отношении.

 

Пример 14. Рассчитайте эффективные процентные ставки по депозитам и определите наиболее выгодный для вкладчика:

а) годовой процент 50%, периодичность начисления один раз в квартал;

б) годовой процент 45%, периодичность начисления 12 раз в год;

в) годовой процент 55%, периодичность начисления один раз в год.

Решение:

а) ;

б) ;

в)

Для вкладчика наиболее выгодный первый депозит (60,18%)

 

Пример 15.Рассчитайте годовой темп инфляции, если:

а) ежемесячный темп инфляции 5%;

б) темп инфляции в первом квартале – 15%, во втором – 10%, в третьем – 20%, в четвертом – 25%.

Решение:

а) ;

б) .

 

При подготовке контрактов может возникнуть необходимость и в решении обратной задачи – в определении j по заданным значе­ниям i и m.Находим

Эффективная процентная ставка используется при расчете доходности валютных депозитов:

,

где: - курс валюты на конец года, руб./долл.;

- курс валюты на начало года, руб./долл.;

- годовая процентная ставка по валютному депозиту.

 

Пример 16. Рассчитайте рублевую доходность валютного депозита и сравните ее с доходностью рублевого депозита, если курс на начало года 28 руб./долл., курс на конец года 30 руб./долл., процентная ставка по валютному депозиту 7%, периодичность начисления 4 раза в год, процентная ставка по рублевому депозиту 15%, периодичность начисления 12 раз в год.

Решение:

 

Доходность валютного депозита:

Доходность рублевого депозита:

Доходность рублевого депозита выше, поэтому вкладчику выгоднее рублевый депозит.

 

Пример 17. Рассчитайте наращенные суммы за год и определите какой депозит выгоднее вкладчику, если первоначальная сумма депозита 1000 рублей.

а) процент в расчете на месяц 5%, используется схема сложного процента;

б) процент в расчете на квартал 16%, используется схема сложного процента;

в) процент в расчете на месяц 6%, используется схема простого процента.

Решение:

а) руб.

б) руб.

в) руб.